tgφ = ![]()
![]() - луч под углом
- луч под углом ![]()
y = 0 → rsinφ = 0 | : r
sinφ = 0
φ = 0
|
0 |
|
![]()
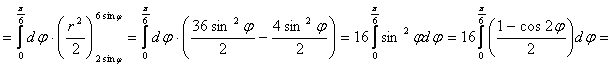
![]()
![]()
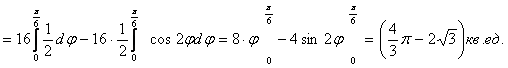
Ответ: ![]()
Задача 8.15.
Условие: Пластинка ![]() задана
ограничивающими ее кривыми,
задана
ограничивающими ее кривыми, ![]() - поверхностная
плотность. Найти массу пластинки.
- поверхностная
плотность. Найти массу пластинки.
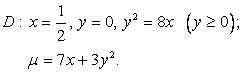
Решение: ![]() - масса
пластинки.
- масса
пластинки.
|
y
x = y2 = 8x (y ≥ 0) 0 y = 0 x |
|
![]()
![]()
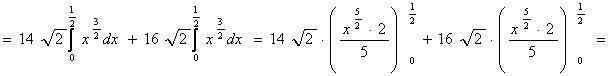
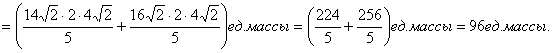
Ответ: 96 ед. массы.
Задача 9.15.
Условие: Пластинка D задана неравенствами, m - поверхностная плотность. Найти массу пластинки.
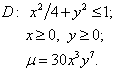
Решение: ![]() - масса пластинки.
- масса пластинки.
![]() - уравнение эллипса с полуосями a = 2,
b = 1;
- уравнение эллипса с полуосями a = 2,
b = 1;
![]() - множество точек внутри эллипса.
- множество точек внутри эллипса.
|
1 0 - 2 2 x - 1 |
Так как область интегрирования круговой сектор, то перейдём к обобщённым полярным координатам:
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.