Свойства двойного интеграла:
1. Если функции f(x,y) и φ(x,y) интегрируемы в области S, то в этой области интегрируемы их сумма и разность f±φ, и верно равенство:
![]() .
.
2. Если С=const, то
![]() .
.
3. Если область S можно представить в виде S=S1US2, S1∩S2=пустому множеству, то
![]() .
.
4. Если функции f и φ интегрируемы в области S и f≤φ в этой области, то
![]() .
.
5. Если функция f интегрируема в области S, то | f| также интегрируема в этой области:
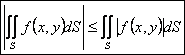 .
.
6. Если
в области S m≤f(x,y)≤М, где mи M – числа, то ![]() ,
где S – площадь
области S.
,
где S – площадь
области S.
Свойства тройного интеграла аналогичны свойствам двойного интеграла.
Вопрос 3. Теорема о среднем для двойного и тройного интегралов.
Теорема о среднем значении для двойного интеграла: Если функция f(P) непрерывна в ограниченной замкнутой области D, то найдется по крайней мере одна точка Pc в области D такая, что будет справедлива формула
![]() ,
,
где S– площадь области D.
Теорема о среднем значении для тройного интеграла: Если функция f(P) непрерывна в замкнутой кубируемой в области Ω, то найдется точка Pc€Ω, такая, что будет справедлива формула
![]()
где V – объем области Ω.
Вопрос 4. Вычисление двойных интегралов двумя последовательными интегрированиями (случай прямоугольной области).
Пусть область R – замкнутый прямоугольник со сторонами, параллельными осям координат R={(x,y): a≤x≤b, c≤y≤d}.
Пусть функция f
непрерывна и неотрицательна в области R.
Двойной интеграл ![]() равен объему
цилиндрического тела с основанием R,
ограниченного поверхностью z=f(x,y).
равен объему
цилиндрического тела с основанием R,
ограниченного поверхностью z=f(x,y).
С другой стороны, объём тела можно вычислить: 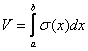 , где σ(x) –
площадь сечения данного тела плоскостью, перпендикулярной оси Ox. По условию
, где σ(x) –
площадь сечения данного тела плоскостью, перпендикулярной оси Ox. По условию 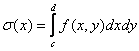 , тогда
, тогда 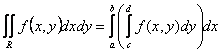 . Полученный интеграл называется
повторным. Его можно записать в виде:
. Полученный интеграл называется
повторным. Его можно записать в виде: 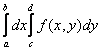 .
Тогда получаем
.
Тогда получаем 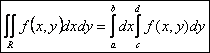 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.