26r2 – 2
● -52x – 2 → - 52rcosφ – 2
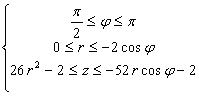
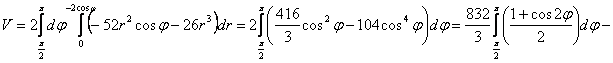
![]()
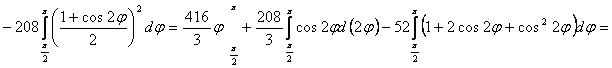
![]()
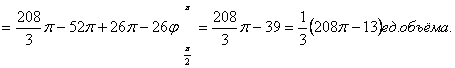
Ответ: ![]()
Задача 15.15.
Условие: Найти объем тела, заданного неравенствами.
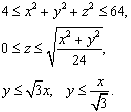
Решение:
● x2 + y2 + z2 = 4, x2 + y2 + z2 = 64 – уравнение сфер с радиусами 2 и 8 соответственно.
● ![]() - верхняя часть
конуса.
- верхняя часть
конуса.
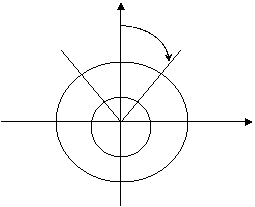
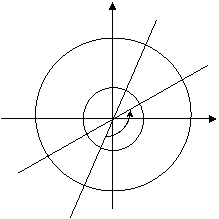 y z
y z
![]() θ
θ
![]()
![]()
0 0
φ 2 8 x y
![]()
Перейдем к сферической системе координат:
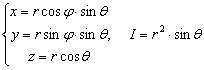 .
.
● ![]() → rsinφ∙sinθ
=
→ rsinφ∙sinθ
= ![]() rcosφ∙sinθ
rcosφ∙sinθ
tgφ=![]()
tφ=![]()
● ![]() → rsinφ∙sinθ
=
→ rsinφ∙sinθ
= ![]() rcosφ∙sinθ
rcosφ∙sinθ
tgφ=![]()
tφ=![]()
● ![]() → r2cos2θ =
→ r2cos2θ = ![]() ( r2cos2φ∙sin2θ
+ r2sin2φ∙sin2θ)
( r2cos2φ∙sin2θ
+ r2sin2φ∙sin2θ)
r2cos2θ = ![]() r2sin2θ
r2sin2θ
cos2θ = ![]() sin2θ
sin2θ
cosθ = ![]() sinθ
sinθ
θ = arctg ![]() .
.
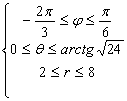
![]()
![]()
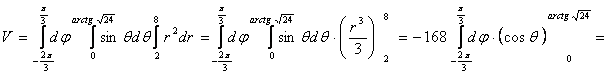
![]()
![]()
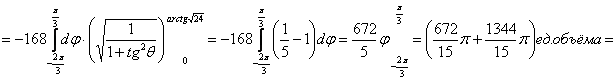
=134,4 π ед.объёма.
Ответ: 134,4 π ед.объёма.
Задача 16.15.
Условие: Тело V задано ограничивающими его поверхностями, m - плотность. Найти массу тела.
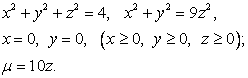
Решение:
● x2 + y2 + z2 = 4 – уравнение сферы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.