Кратные интегралы, страница 4

Формулу перехода от интеграла в декартовых координатах к интегралу в полярных координатах можно записать так:

.

Вопрос 9. Тройной интеграл в цилиндрических координатах.

В цилиндрической системе координат положение точки в пространстве определяется тремя числами r,φ,z, где r и φ - полярные координаты проекции точки на плоскость xOy, а z – аппликата точки. Числа r,φ,z называются цилиндрическими координатами точки. Ясно, что 0≤r≤+∞, 0≤φ≤2π, -∞≤z≤+∞. Цилиндрические координаты связаны с декартовыми следующими формулами x=rcosφ, y=rsinφ, z=z.

Формула перехода от тройного интеграла в прямоугольных координатах к интегралу в цилиндрических координатах принимает вид:

.

Вопрос 10. Тройной интеграл в сферических координатах.

В сферической системе координат положение точки в пространстве определяется тремя числами r,φ,θ где r – расстояние от начала координат до точки, φ - угол между осью Ox и проекцией радиуса-вектора точки на плоскость xOy, а θ - угол между осью Oz и радиусом-вектором точки, отсчитываемой от оси Oz. Ясно, что 0≤r≤+∞, 0≤φ≤2π, 0≤ θ≤π.

Сферические и декартовые координаты связаны следующими соотношениями: x=rsinθ cosφ, y=rsinθ sinφ, z=rcosθ. Якобиан равен: I=r²sinθ.

Формула перехода от тройного интеграла в прямоугольных координатах к интегралу в сферических координатах принимает вид:

.

РАСЧЕТНЫЕ ЗАДАНИЯ

Задача 1.15.

Условие: Изменить порядок интегрирования .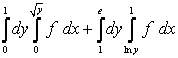

Решение:Область D ограничена линиями:   y = 0,    y = 1,    x = 0,    x = ,   y = e,   x = ln y,   x = 1.

x=    x=ln y                      y                                                           y = e                                                         y = 1                      0                         y = 0              x

x =  => x2 = y x = ln y => ex = y  = = .