Кратные интегралы, страница 7

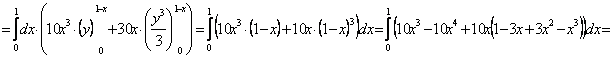
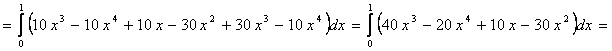
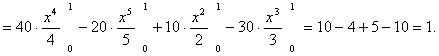
Ответ:    1.

Задача 6.15.

Условие: Найти площадь фигуры, ограниченной данными линиями.

Решение:

y                           0                                          y = -4x y = 32-x2

Найдём точки пересечения графиков y = 32 - x2 и y = - 4x: - x2 + 4x + 32 = 0 | · (- 1)   x2 - 4x - 32 = 0 D = 16 + 128 = 144 > 0, x1 ≠ x2 ; x1 = 8;     y1 = - 32; x2 = - 4;   y2 = 16. Тогда,

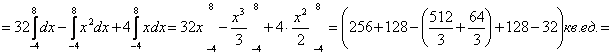
Ответ: 288 кв.ед.

Задача 7.15.

Условие: Найти площадь фигуры, ограниченной данными линиями.

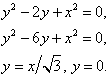
Решение:                           Выделим полный квадрат:

Ÿ  y² – 2y + x² = y² – 2·y·1 + 1 – 1 + x² = (y – 1)² + x² – 1.

(y – 1)² + x² = 1 – уравнение окружности с центром в т. (0,1) и R = 1.

Ÿ  y² – 6y + x² = y² – 2·y·3 + 9 – 9 + x² = (y – 3)² + x² – 9.

(y – 3)² + x² = 9 – уравнение окружности с центром в т. (0,3) и R = 3.

Перейдём к полярной системе координат, т.к. область интегрирования – круговой сектор:

, I = r.

Ÿ  y² – 2y + x² = 0   →   r²sin²φ – 2rsinφ + r²cos²φ = 0

r² – 2rsinφ = 0   | : r

r - 2sinφ = 0

r = 2sinφ

Ÿ  y² – 6y + x² = 0   →   r²sin²φ – 6rsinφ + r²cos²φ = 0

r² – 6rsinφ = 0   | : r

r - 6sinφ = 0

r = 6sinφ

Ÿ     →   rsinφ =