Кратные интегралы, страница 9

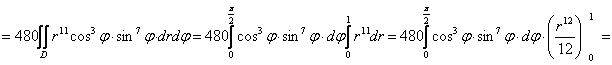
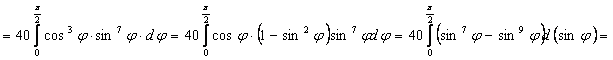
Ответ:   1 ед. массы.

Задача 10.15.

Условие: Найти объем тела, заданного ограничивающими его поверхностями.

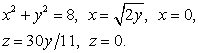
Решение:          x² + y² = 8 – уравнение цилиндра.

 - уравнение цилиндра параболического.

2y + y2 = 8 y2 + 2y – 8 = 0 D = 4 + 32 = 36, y1 ≠ y2 y1 = - 4;   y2 = 2.	y                                                     x2 + y2 = 8                                        2       x	z                          0                                   y

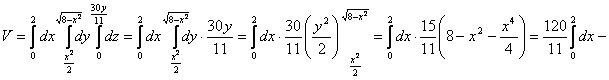
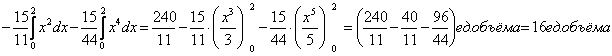
Ответ:   16 ед. объёма.

Задача 11.15.

Условие: Найти объем тела, заданного ограничивающими его поверхностями.

Решение:     ● x² + y² = 6x – уравнение цилиндра.

x² + y² - 6x = 0

x² – 2x·3 + 18 – 18 + y² = 0

(x – 3)² + y² = 18 - уравнение окружности с радиусом .

● z = x² + y² – 36 – уравнение эллиптического параболоида, который обращен вверх.

x² + y² = 36 – уравнение окружности с R = 6.