Кратные интегралы, страница 10

y                                                                                     (x–3)2+y2=18                     0         φ                                                            x x2 + y2 = 36                                              -

Так как область интегрирования круговой сектор, то перейдём к полярным координатам:

, I = r.

● x² + y² = 6x   →   r²cos²φ + r²sin²φ = 6r cosφ

r² = 6r cosφ

r = 6cosφ

● x² + y² = 36   →   r²cos²φ + r²sin²φ = 36

r² = 36

r = 6

Найдём угол φ:

6 = 6 cosφ | : 6

1 =  cosφ | :

φ =

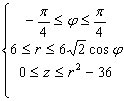
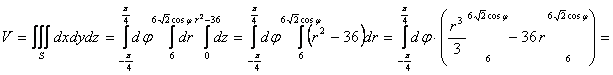
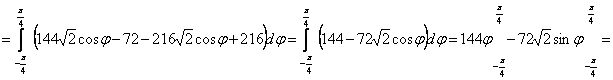
Ответ:   .

Задача 12.15.

Условие: Найти объем тела, заданного ограничивающими его поверхностями.

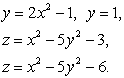
Решение:y = 2x² – 1 – уравнение параболического цилиндра.

z = x² – 5y² – 3;  z = x² – 5y² – 6 – уравнения гиперболических параболоидов.

y                                              y = 2x2 – 1                                                y = 1                                                       x                x=-1           x=1