Примерные экзаменационные задания по дисциплине "Высшая математика"

№1. Дать определение линейного оператора.

Линейным оператором в линейном n-мерном пространстве  называется всякое отображение  пространства  в себя, удовлетворяющее условиям линейности: , где  и  - произвольные векторы линейного пространства , - любое действительное число.

№3. Доказать, что если А-собственный вектор, то СА, где С-константа, тоже собственный вектор.

Пусть задано n-мерное линейное пространство R и пусть число  и ненулевой вектор , таковы что: . Тогда - собственное число, а x – собственный вектор, соответствующий числу .

№4. Решить матричное уравнение:

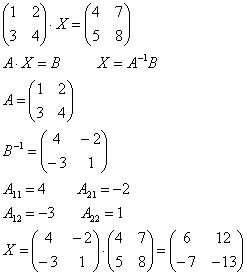
МАТЕМАТИЧЕСКИЙ АНАЛИЗ

№1. Односторонние производные.

Правой производной  функции  в данной точке x называется величина

и левой производной  - величина

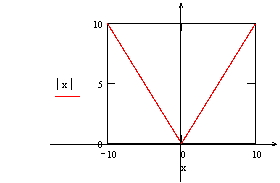
Следующий пример показывает, что существуют функции, которые имеют в точке x и правую и левую производную, но не имеют производной в этой точек.

,  Для этой функции отношение равно 1, если  и равно -1, если . Поэтому функция  в точке  имеет правую производную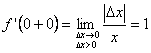  

и левую производную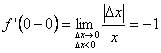

№3. Бесконечно малые функции и их свойства.

При изучении свойств пределов функции особую рольиграют функции, пределы которых при стремлении аргумента к какой-либо точке равны нулю.

Функция f(х) называется бесконечной малой при х->а, если lim f(x) = 0, то есть для любого числа е>0 существует >0 такое, что из |x-a|< следует |f(x)|<.

Если функция f (х) и g(х) являются бесконечно малыми, то функция f(х) + g(х) тоже бесконечно малая.

Данное утверждение распространяется на случай алгебраической суммы любого конечного числа бесконечно малых.

№5. Найти производную: