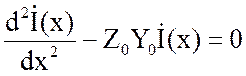Четырехполюсники. Электрические цепи с распределенными параметрами. Магнитные цепи. Магнитные цепи при периодических процессах, страница 5

.                                   (2.5)

Решение уравнения (2.4) в общем виде:

,                                   (2.6)

где     ,  - комплексные коэффициенты, определяемые из граничных условий на входе или выходе линии;

           -                                     (2.7)

комплексное число, называемое коэффициентом распространения на единицу длины.

Решение для тока находится из первого уравнения системы (2.3):

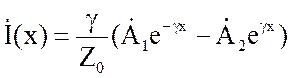, или

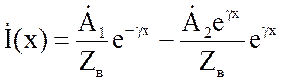,                                        (2.8)

где 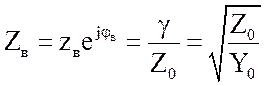, Ом -  волновое сопротивление линии.                                                                                                  (2.9)

2.4. Бегущие волны. Параметры волны

Решение (2.6) с подстановкой в (2.7) можно представить в виде:

,                              (2.10)

где , .

Мгновенное значение напряжения в точке х равно мнимой части выражения  и имеет вид:

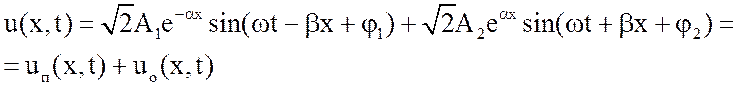          (2.11)

Первое слагаемое уравнения (2.11)  представляет затухающую волну напряжения, амплитуда которой убывает с увеличением координаты х по закону экспоненты . Фаза волны при фиксированном моменте времени изменяется на единице длины на величину b. Убывание амплитуды волны вдоль линии обусловлено потерями в линии, а изменение фазы – конечной скоростью распространения волны.

На рис. 2.2 изображены графики распределения волны напряжения, соответствующие двум последующим моментам времени t₁ и t₂. За отрезок времени  точка «а» волны напряжения, находящаяся в нулевой фазе, переместилась на расстояние  в направлении возрастания х. С течением времени волна перемещается от начала линии к концу; она называется прямой волной.

Скорость перемещения волны (точки с неизменной фазой колебания), называемой фазовой скоростью, равна

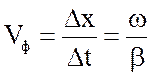.                                                (2.12)

Для однородной линии фазовая скорость постоянна.

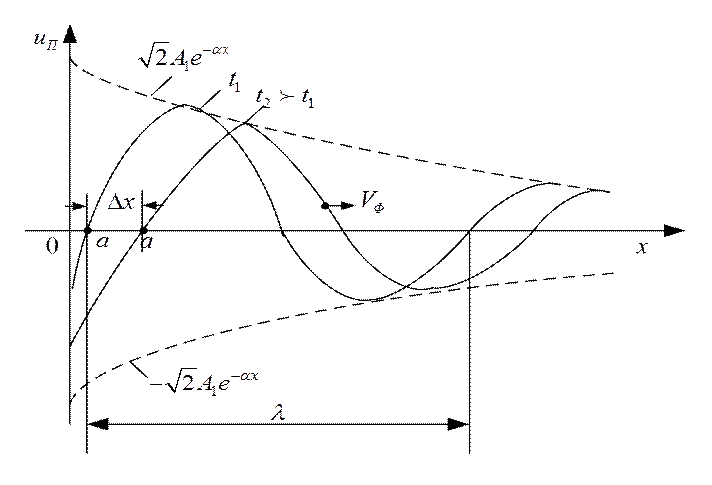
Рис. 2.2. График распределения прямой волны напряжения для двух моментов времени t₁ и t₂

Вторым параметром бегущих волн является длина волны. Это расстояние между двумя ближайшими точками, разность фаз колебаний в которых равна 2p:

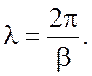                                            (2.13)

За время, равное периоду колебаний Т, бегущая волна перемещается на расстояние, равное длине волны:

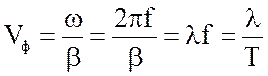.                                          (2.14)

Второе слагаемое  напряжения (2.11) представляет собой бегущую волну напряжения, перемещающуюся в обратном направлении: от конца линии к ее началу. Она называется обратной, или отраженной волной.

На рис. 2.3 изображены графики обратной волны для двух моментов времени t₁ и t₂. Амплитуда обратной волны затухает в направлении движения волны. Фазовая скорость направлена в сторону уменьшения координаты х.

В воздушных линиях фазовая скорость близка к скорости света  м/с. В кабельных линиях фазовая скорость тем меньше, чем выше диэлектрические свойства изоляции.

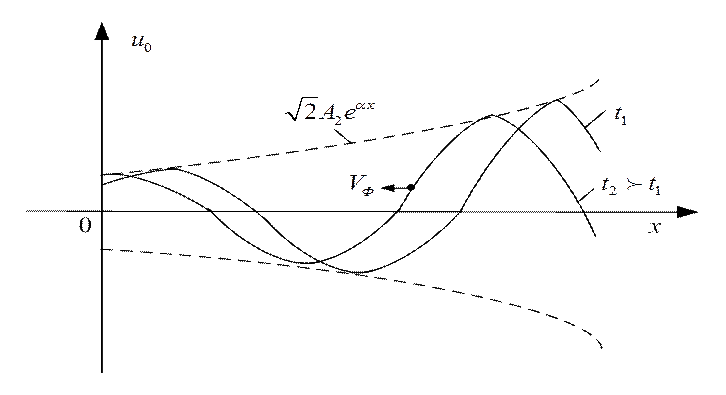
Рис. 2.3. График распределения обратной волны напряжения для двух моментов времени t₁ и t₂

Итак, напряжение в любой точке линии является наложением прямой и обратной бегущих волн.

Согласно решениям (2.6) и (2.8) напряжение и ток в комплексной форме можно представить:

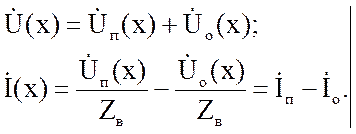                              (2.15)

где     ,  - прямые волны соответственно напряжения и тока;

          ,  - обратные волны.

Как следует из (2.15), прямая и обратная волны напряжения суммируются, прямая и обратная волны тока вычитаются.

Мгновенные значения бегущих волн тока:

- прямая 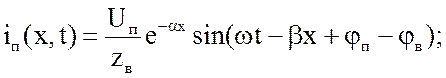                                      (2.16)

- обратная

2.5. Вторичные параметры однородной линии

К вторичным параметрам линии относят коэффициент распространения g (2.7) и волновое сопротивление Z_в (2.9). Они входят во все расчетные соотношения волновых процессов в линии и определяются через первичные параметры r₀, L₀, g₀, С₀.

Коэффициент распространения

                          (2.17)