Из принципа непрерывности магнитного поля (линии магнитной индукции непрерывны и замкнуты) следует, что поток вектора магнитной индукции сквозь замкнутую поверхность равен нулю:
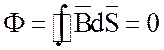. (3.11)
Отсюда следует, что в разветвленной магнитной цепи магнитный поток, подходящий к месту разветвления, равен сумме потоков, отходящих от места разветвления. В этом случае магнитный поток Ф, подобно току в электрической цепи, подчиняется первому закону Кирхгофа:
, (3.12)
т.е. алгебраическая сумма магнитных потоков в узле равна нулю.
Итак, к расчету магнитных цепей применимы первый и второй законы Кирхгофа (3.12), (3.8), для линейной магнитной цепи – также и закон Ома (3.10). Так как в основном магнитные цепи нелинейны, к их расчету применимы известные графические и графоаналитические методы расчета нелинейных электрических цепей постоянного тока с построением веберамперных характеристик участков цепи Ф = f(UМ), подобных вольтамперным характеристикам для электрических цепей.
3.4. Особенности расчета магнитных цепей
При анализе магнитных цепей рассматриваются две задачи: прямая и обратная. В обоих случаях задаются геометрические параметры магнитопровода, основные кривые намагничивания В(Н) ферромагнитных материалов.
В прямой задаче задается значение магнитного потока Ф или магнитной индукции в воздушном зазоре и требуется определить намагничивающую силу F = Iw.
В обратной задаче по заданному значению намагничивающей силы требуется определить поток (или потоки в разветвленной магнитной цепи). Задача решается значительно сложнее, т.к. требует построения веберамперной характеристики цепи, зависимости F = f(Ф) или Ф = f(F).
Для построения такой
характеристики приходится задаваться несколькими значениями потока Ф, находить
соответствующие им значения F,
решая, таким образом, несколько прямых задач. По полученной зависимости
F = f(Ф) или Ф = f(F) графически находится нужное решение от заданной
F = Iw.
3.5. Примеры решения прямой и обратной задач в неразветвленной магнитной цепи
П р и м е р 3. 1
Прямая задача Геометрические размеры сердечника и величина воздушного зазора указаны на рис. 3.4.
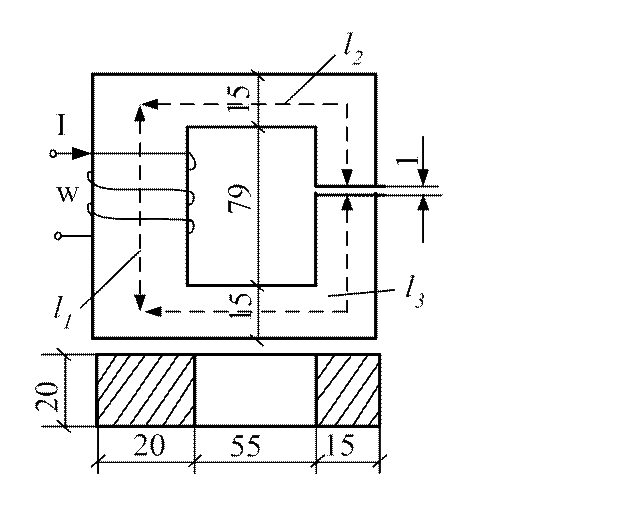
Рис. 3.4. Магнитная цепь
Сердечник выполнен из
электротехнической стали, кривая намагничивания которой В(Н) приведена на рис. 3.5.
Число витков катушки
w = 500.
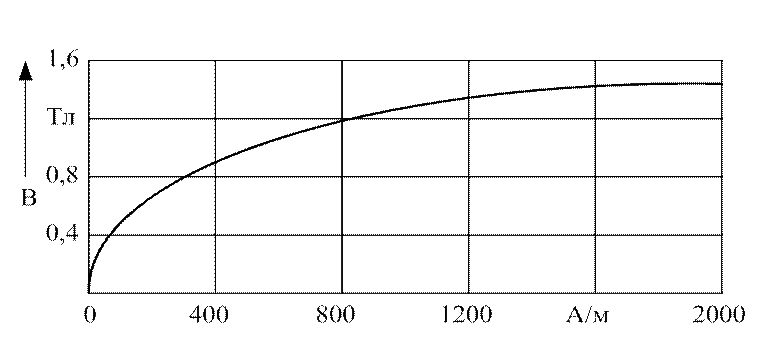
Рис. 3.5. Кривая намагничивания стали
Требуется определить ток в катушке при значении магнитной индукции в воздушном зазоре Вв = 1,2 Тл.
Р е ш е н и е
Разбиваем магнитопровод по средней линии на участки одинакового сечения l1, l2, l3 плюс воздушный зазор lв. Определяем длину и поперечное сечение каждого участка:
l1 = 0,085 м; l2 = l3 = 0,1 м; lв = 1×10-3 м;
S1 = 4×10-4 м2; S2 = S3 = Sв =4×10-4 м2.
Записываем уравнение по второму закону Кирхгофа для магнитной цепи
Решение находится в следующей последовательности.
Определяем значение магнитного потока в магнитопроводе
Вб
и значения индукции на всех участках:
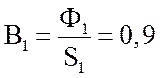Тл; 
Тл.
По кривой В(Н) (рис. 3.5) определяем напряженности в стержнях:
А/м; 
А/м.
В воздушном зазоре 
А/м.
Из уравнения цепи находим намагничивающую силу
А
и ток в катушке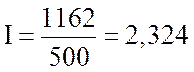 
А.
П р и м е р 3. 2. Обратная задача
Для магнитной цепи (рис. 3.4), размеры участков которой и марка стали те же, что в примере 3.1, требуется определить магнитный поток в сердечнике при заданной намагничивающей силе Iw = 860 А.
Р е ш е н и е
Имеем одно и то же уравнение цепи
,
в котором четыре неизвестных (
).
Решаем задачу построением зависимости F = f(Ф), задаваясь несколькими значениями Ф и решая для каждого значения прямую задачу в нахождении F. Решения записываем в табл. 3.1.
Таблица 3.1
Результаты расчетов прямой задачи
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.