Четырехполюсники. Электрические цепи с распределенными параметрами. Магнитные цепи. Магнитные цепи при периодических процессах, страница 4

Параллельно-последовательное соединение

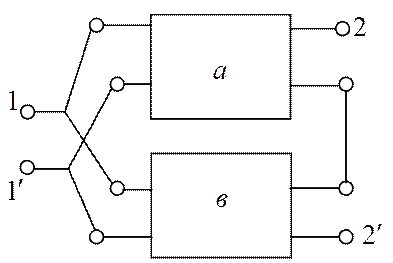
Рис. 1.12. Параллельно-последовательное соединение

Уравнения записываются в системе F – параметров. В этом случае матрица [F] соединения равна сумме [F] матриц – соответствующих четырехполюсников

П р и м е р 1. 7

По матрицам одноэлементных четырехполюсников, найти матрицу [А]
Т – образной схемы (рис.1.13)

  

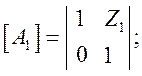
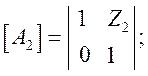
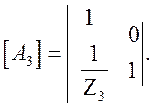
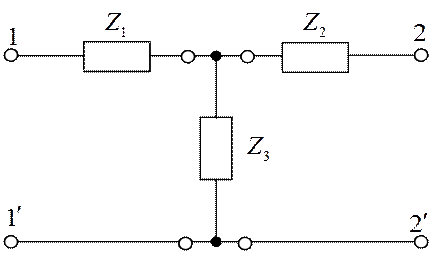
Рис. 1.13. Составной четырехполюсник

Р е ш е н и е

Матрица соединения двух элементов:

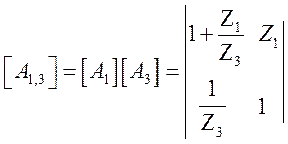– есть матрица Г – образного четырехполюсника (рис. 1.14)

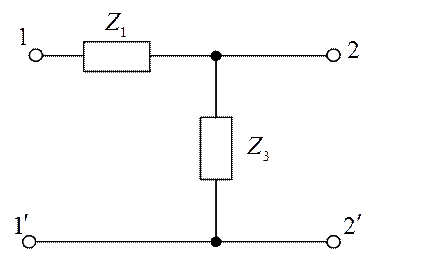
Рис. 1.14.

Произведение матриц:

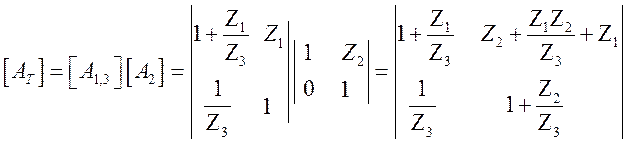
определяет матрицу Т – образной схемы (рис. 1.13).

2. Электрические цепи с распределенными параметрами

2.1. Основные определения

Электрическими цепями с распределенными параметрами называют цепи, в которых электрическое и магнитное поля и потери энергии распределены по всей длине цепи. Напряжения и токи в таких цепях непрерывно изменяются при переходе от одной точки (сечения) к другой. Электромагнитные процессы в них носят волновой характер, и приходится учитывать конечную скорость распространения электромагнитных волн. Особенностями анализа цепей с распределенными параметрами является то, что напряжения и токи являются функциями двух переменных: времени t и пространственной координаты х вдоль цепи. К этому классу цепей относятся высоковольтные линии электропередачи, воздушные и кабельные линии связи, рельсовые цепи, обмотки трансформаторов и электрических машин, высокочастотные кабели, соединяющие антенны с приемопередаточной аппаратурой и др.

В данном разделе рассматриваются установившиеся режимы в цепях с распределенными параметрами на примере длинной линии при условии равномерного распределения параметров по ее длине. Такая линия называется однородной. Понятие «длинная линия» применяется при соизмеримости протяженности линии с длиной волны установившегося режима от источника синусоидального напряжения.

2.2. Параметры и уравнения длинной линии

Распределенные параметры однородной двухпроводной линии на единицу длины: r₀ – активное сопротивление двух проводов; L₀ – индуктивность; g₀ – проводимость изоляции; С₀ – емкость между проводами – носят название первичных параметров.

Длинную линию можно разбить на элементарные участки длиной dx
(рис. 2.1), где х – расстояние от начала линии, и представить элементарный участок в виде четырехполюсника с параметрами продольного плеча r₀dx, L₀dx и параметрами поперечного плеча g₀dx, C₀dx.

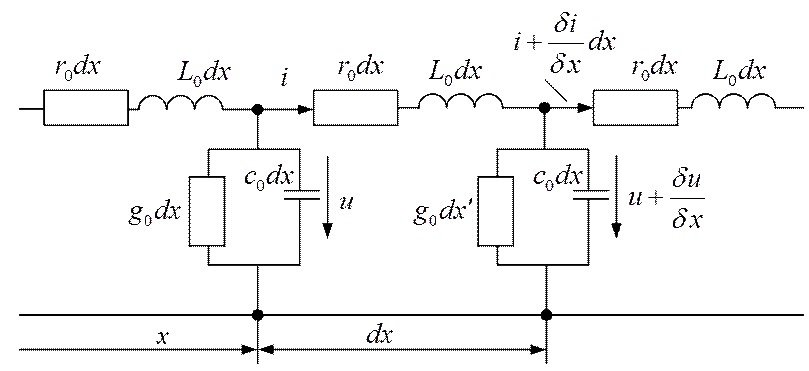
Рис. 2.1. Схема замещения элементарного участка цепи с распределенными параметрами

Напряжение и ток в начале участка обозначены соответственно u и i, напряжение и токи в конце участка – 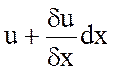и .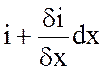

Частные производные  и  определяют скорость изменения напряжения и тока вдоль участка. Процессы на участке цепи описываются уравнениями по законам Кирхгофа для мгновенных значений:

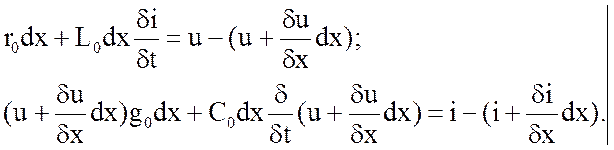              (2.1)

После упрощения и сокращения уравнений (2.1) на dx они принимают вид:

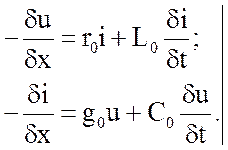                                                (2.2)

и являются основными дифференциальными уравнениями цепи с распределенными параметрами.

В установившихся режимах закон изменения напряжения и тока в функции времени известен (задан источником), что позволяет найти точное решение системы уравнений (2.2) и получить зависимость распределения напряжения и тока вдоль линии.

2.3. Установившийся синусоидальный режим

В режиме синусоидальных напряжений и токов основные дифференциальные уравнения записываются для комплексных действующих значений  и , которые не зависят от времени и являются функциями только координаты х:

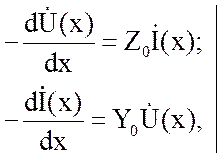                                                 (2.3)

где      – комплексное продольное сопротивление на единицу длины;

           – комплексная поперечная проводимость на единицу длины.

Уравнения (2.3) путем дифференцирования и преобразования сводятся к двум линейным дифференциальным уравнениям второго порядка:

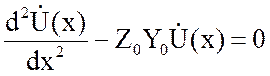;                               (2.4)