В расчетных уравнениях (2.28) гиперболические функции от мнимого аргумента преобразуются в тригонометрические функции:
![]() ,
,
и расчетные уравнения для линии без потерь принимают вид:
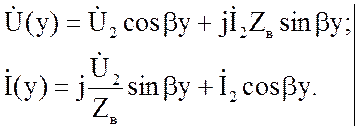 (2.43)
(2.43)
Входное сопротивление линии без потерь при произвольной нагрузке:
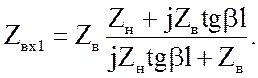 (2.44)
(2.44)
2.11. Режим холостого хода. Стоячие волны
При отсутствии нагрузки в
конце линии (![]() ) ток
) ток ![]() , и
уравнения для режима холостого хода имеют вид:
, и
уравнения для режима холостого хода имеют вид:
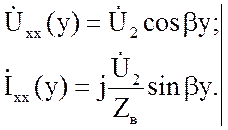 (2.45)
(2.45)
Входное сопротивление линии:
![]() (2.46)
(2.46)
– чисто реактивное, поэтому активная мощность на входе Р1 = 0. В линии возникает режим стоячих волн.
Из (2.45) следует, что действующие значения напряжения и тока являются периодическими функциями координаты у. Графики распределения модулей действующих значений напряжения и тока вдоль линии показаны на рис. 2.9.
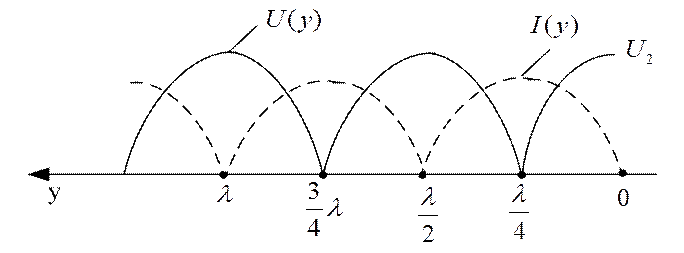
Рис. 2.9. Стоячие волны в режиме холостого хода
Точки линии, в которых напряжение (ток) равно нулю, называются узлами напряжения (тока); точки, в которых напряжение (ток) имеют максимум, называют пучностями напряжения (тока). Узлы и пучности чередуются на отрезках, равных четверти длины волны (λ/4).
Режим стоячих волн
возникает в результате наложения прямых и обратных волн с одинаковой
амплитудой. В режиме холостого хода коэффициент отражения ρ = 1. Это значит,
что ![]() .
.
Если уравнения (2.45) записать в виде
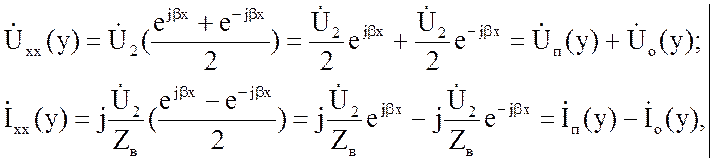 (2.47)
(2.47)
то очевидны равенства 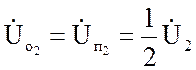 ,
, 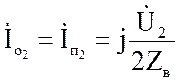 .
.
В точке линии с координатой у = λ/4, β λ/4 = π/2 и
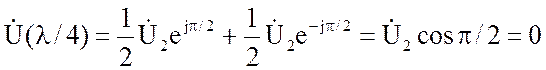 -
узел напряжения;
-
узел напряжения;
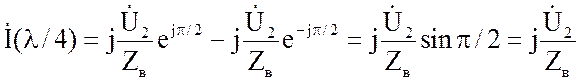 -
пучность тока.
-
пучность тока.
Стоячие волны напряжения и тока (рис. 2.9) сдвинуты относительно друг друга в пространстве на четверть длины волны λ/4, и во времени – на π/2.
В режиме стоячих волн мощность в узлах напряжения и тока равна нулю, в остальных точках линии имеет место только реактивная мощность, так как напряжение и ток сдвинуты по фазе на π/2. В этом случае энергия не передается вдоль линии, а происходит лишь обмен энергией между электрическим и магнитным полями на участках линии, ограниченных узлами напряжения и тока.
Кроме холостого хода, режим стоячих волн возникает при коротком замыкании выхода линии или при чисто реактивной нагрузке.
Расчетные уравнения короткозамкнутой линии:
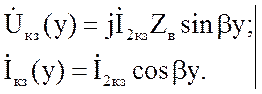 (2.48)
(2.48)
Входное сопротивление короткозамкнутой линии:
![]() . (2.49)
. (2.49)
В зависимости от длины линии l входное сопротивление разомкнутой и короткозамкнутой линии согласно (2.46) и (2.49) могут иметь емкостный или индуктивный характер и изменяться по модулю от -¥ до +¥.
2.12. Примеры расчета волновых процессов в линии
П р и м е р 2. 1
Даны параметры
однородной линии на частоте f= 800 Гц;
r0=10,2 Ом/км; L0=7·10-3 Гн/км; С0=6,8·10-9
Ф/км; g0=1·10-6 См/км.
Требуется определить вторичные параметры линии ZВ и γ, фазовую скорость и длину волны.
Р е ш е н и е
Волновое сопротивление на
частоте ![]()
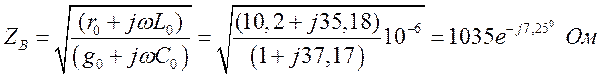 .
.
Коэффициент распространения
![]()
![]() –
коэффициент затухания;
–
коэффициент затухания;
![]() –
коэффициент фазы.
–
коэффициент фазы.
Фазовая скорость 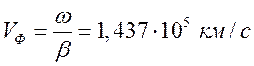 ;
;
длина волны 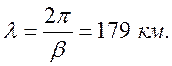
П р и м е р 2. 2
В линии с параметрами п. 2.12.1 длиной l=120
км напряжение на нагрузке ![]()
Требуется определить напряжение ![]() и ток
и ток ![]() в начале
линии, активную мощность в начале и в конце линии и КПД при сопротивлении
нагрузки:
в начале
линии, активную мощность в начале и в конце линии и КПД при сопротивлении
нагрузки:
1) ![]()
2) ![]() .
.
Р е ш е н и е
1. При нагрузке ![]() , ток в
конце линии
, ток в
конце линии 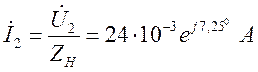 .
.
Напряжение ![]() и ток
и ток ![]() находим по формулам:
находим по формулам:
![]()
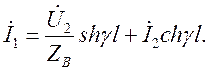
Расчет гиперболических функций:
аргумент ![]()
![]()
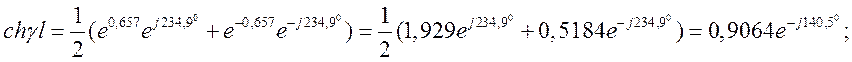
 .
.
Напряжение в начале линии:
![]()
Ток в начале линии:
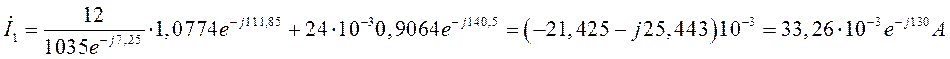
Активная мощность на входе линии:
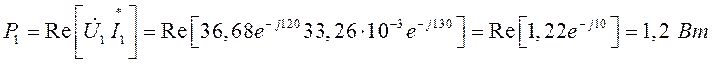
Активная мощность на нагрузке:
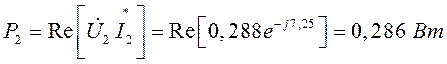 .
.
Коэффициент полезного действия:
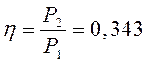
2. В режиме
согласованной нагрузки ![]()
Ток в нагрузке ![]() .
.
Напряжение в начале линии:
![]()
Ток в начале линии:
![]()
Активная мощность на входе и на нагрузке:
![]()
![]()
Собственное затухание линии:
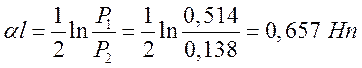 .
.
П р и м е р 2. 3
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.