Достраивается векторная
диаграмма по уравнению (4.7) падением напряжения в индуктивном сопротивлении
рассеяния ![]() (опережает ток
(опережает ток ![]() на
угол
на
угол ![]() ) и падением напряжения на активном
сопротивлении обмотки
) и падением напряжения на активном
сопротивлении обмотки ![]() (совпадает по фазе с током).
(совпадает по фазе с током).
4.3 Схема замещения катушки
Векторной диаграмме (рис.4.4) соответствует схема замещения катушки (рис. 4.5).
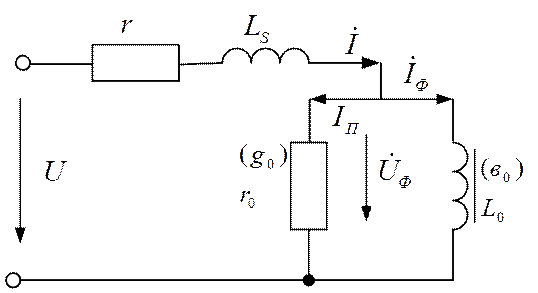
Рис. 4.5. Схема замещения катушки с ферромагнитным сердечником
Участок с двумя
параллельными ветвями отражает физические процессы в сердечнике.
Намагничивающий ток ![]() определяет основной магнитный
поток в сердечнике и связан с ним соотношением
определяет основной магнитный
поток в сердечнике и связан с ним соотношением ![]() , где
, где ![]() – индуктивность намагничивающей ветви.
– индуктивность намагничивающей ветви.
В литературе принято эту
ветвь задавать реактивной проводимостью 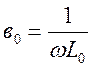 .
.
Ток IП и активное сопротивление r0, активная проводимость g0 другой параллельной ветви замещают потери в стали:
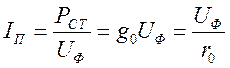 .
.
Параметры последовательной ветви:
r – активное сопротивление обмотки;
LS – индуктивность рассеяния, обусловленная потоком рассеяния.
Катушка с сердечником – нелинейный элемент, поэтому параметры схемы замещения справедливы только для конкретного режима. В общем случае параметры LS, L0(в0), r(g0) – являются функциями тока. Чем больше насыщение сердечника, тем больше поток рассеяния, больше потери в стали, при этом параметр LS увеличивается, индуктивность намагничивающей ветви L0 – уменьшается, увеличивается сопротивление r0.
Нахождение параметров схемы замещения для конкретного режима является довольно трудной задачей. Наибольшие трудности представляет нахождение индуктивности рассеяния. В режимах слабого насыщения сердечника часто потоком рассеяния пренебрегают.
Активное сопротивление обмотки r обычно измеряют постоянным током.
4.4 Примеры расчета параметров схемы замещения
П р и м е р 4. 1
С помощью измерительных
приборов: вольтметра, амперметра, ваттметра определяют 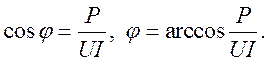
Разделяют потребляемую
мощность на потери в меди РМ и потери в стали: РСТ = Р
- РМ = Р – I2r . Принимая ![]() определяют напряжение
определяют напряжение ![]() из уравнения цепи (4.7) (при LS = 0 )
из уравнения цепи (4.7) (при LS = 0 ) ![]()
Рассчитывают токи:
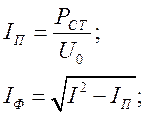
проводимости ветвей:
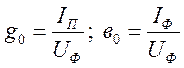
и угол потерь
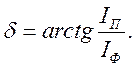
П р и м е р 4. 2
Измерив U, I, P, определив угол φ, потери в стали РСТ, рассчитывают по закону полного тока для магнитной цепи напряженность Нm
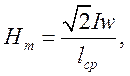
где ![]() –
средняя линия магнитопровода.
–
средняя линия магнитопровода.
По динамической кривой намагничивания для данного материала определяют Вm и Фm = Вm S, где S – сечение магнитопровода.
Принимают поток
синусоидальным Ф(t) = Фmsinωt и находят 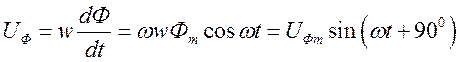 ,
где
,
где ![]()
Действующее значение напряжения
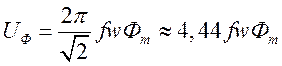 (4.9)
(4.9)
В комплексной форме ![]()
Далее рассчитывают IП, g0, IФ, в0, δ – как в первом варианте.
Ток и входное напряжение согласно векторной диаграмме (рис. 4.4) записывают в комплексной форме:
![]()
Из уравнения цепи (4.7) определяют
![]() и параметр LS.
и параметр LS.
П р и м е р 4. 3
Исходными данными являются максимальное значение индукции Вm (магнитного потока Фm), размеры магнитопровода, материал, число витков обмотки, частота питающего напряжения.
Существуют таблицы или кривые, определяющие зависимости удельной мощности потерь Р0 и удельной намагничивающей мощности Q0 от частоты f и магнитной индукции Bm.
Рассчитав массу сердечника G, находят потери в стали PСТ = Р0G и намагничивающую мощность QСТ = Q0G.
Далее находят
![]()
составляющие тока
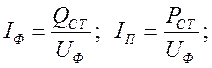
проводимости
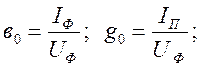
ток в катушке ![]() и
угол потерь
и
угол потерь 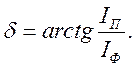
Активное сопротивление обмотки известно. Потоком рассеяния иногда задаются в процентах (%) от основного потока. Уточняют параметры из эксперимента.
П р и м е р 4. 4
Катушка с числом витков w = 500 и магнитопроводом из электротехнической стали включена в сеть с напряжением U = 220 В. Ток катушки I = 10 А, активная мощность Р = 1500 Вт. Сопротивление обмотки постоянному току r = 10 Ом. Амплитуда потока в магнитопроводе Фm = 10-3 Вб. Составить схему замещения катушки f = 50 Гц.
Решение
Определим напряжение на намагничивающей ветви
![]() .
.
Разделяем потери ![]() Вт.
Вт.
Находим составляющие тока:
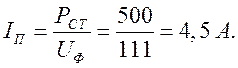 ;
; ![]()
![]() ,
,
и параметры 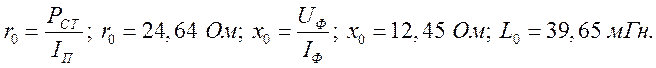
Полное 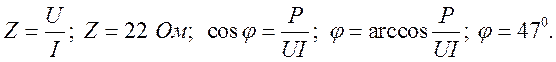
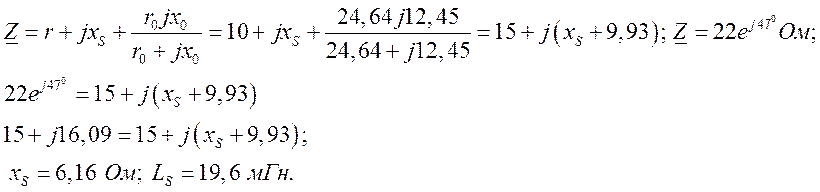
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.