Четырехполюсники. Электрические цепи с распределенными параметрами. Магнитные цепи. Магнитные цепи при периодических процессах, страница 12

Ф×103, Вб	В1, Тл	В2= В3= =Вв, Тл	Н1, А/м	Н2=Н3, А/м	Нв, А/м	Н1l1, А	2Н2l2, А	Нвlв, А	F=Iw, А
30	0,75	1,0	280	500	8×105	23,8	100	800	923
24	0,6	0,8	200	300	6,4×105	17	60	640	717
27	0,675	0,75	250	400	7,2×105	21,2	80	720	821,5

Так как магнитное сопротивление воздушного зазора значительно больше магнитного сопротивления сердечника, в первом приближении принимаем А.

Отсюда находим

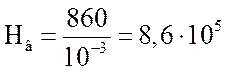 А/м,

 Тл,

 Вб

В этом приблизительном расчете пренебрегли магнитными падениями напряжения в сердечнике, поэтому для расчета принимаем значение , решаем прямую задачу и находим F₁ = 923 А. Значению  Вб соответствует F₂ = 717 А.

Следовательно, Ф₃ выбираем в пределах , а именно,  Вб, и определяем F₃ = 821,5 А.

На рис. 3.6 построена зависимость F = f(Ф) по трем точкам расчета и графически найдено решение: при заданной F = 860 А поток в сердечнике  Вб.

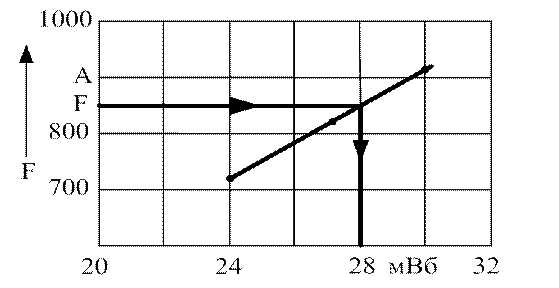
Рис. 3.6. Графическое решение обратной задачи

3.6. Расчет разветвленных магнитных цепей

При расчете разветвленных магнитных цепей с одной намагничивающей силой положительные направления магнитных потоков определяются положительным направлением намагничивающей силы (рис. 3.7). Если в такой цепи действуют несколько намагничивающих сил, выбор положительных направлений потоков затруднителен, их выбирают произвольно.

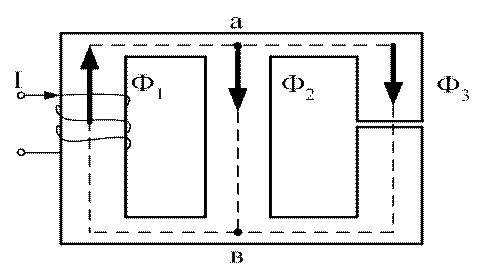
Рис. 3.7. Выбор направления потоков от действия одной н. с.

Наибольшую трудность представляет решение обратной задачи с несколькими намагничивающими силами. В большинстве случаев разветвленная магнитная цепь имеет два узла (рис. 3.). Задача решается методом двух узлов для нелинейных цепей. Для каждой ветви рассчитывается веберамперная характеристика – зависимость магнитного потока ветви от магнитного напряжения между точками разветвления . Характеристики всех ветвей строятся в одном масштабе на графике и решение находится графически по первому закону Кирхгофа.

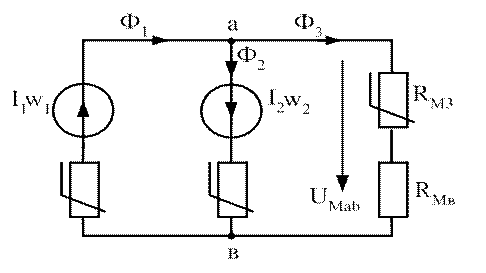
Так, для схемы (рис. 3.8, а) выбираем направления магнитных потоков, рисуем схему – аналог электрической цепи (рис. 3.8, б).

 

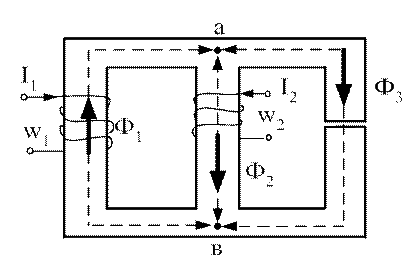
                                  а)                                                              б)

Рис. 3.8. а) Разветвленная магнитная цепь; б) Схема-аналог электрической цепи

Записываем уравнения по законам Кирхгофа:

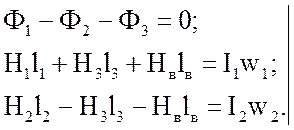
Выразим общее напряжение U_Mab через напряжения каждой ветви:

 – для третьей ветви;

 – для первой ветви;

 – для второй ветви.

Необходимо рассчитать зависимости Ф₁ = f₁(U_Mab), Ф₂ = f₂(U_Mab),
Ф₃ = f₃(U_Mab).

Для этого задаемся значениями потоков Ф_k (или магнитных индукций В_k, а потоки находим по формуле ) и рассчитываем соответствующие значения магнитного напряжения U_Mab. Расчет проводим в форме таблиц. Для отдельных ветвей таблицы имеют вид:

Таблица 3.2

Расчет зависимости Ф₁ = f₁(U_Mab)

Таблица 3.3

Расчет зависимости Ф₂ = f₂(U_Mab)

Таблица 3.4

Расчет зависимости Ф₃ = f₃(U_Mab)

Ф3, Вб	, Тл	Н3=f(В3), А/м	, А	, А/м	, А	, А
…

По полученным данным строимся кривые (рис. 3.9). Искомое решение определяется по закону Кирхгофа Ф₁ = Ф₂ + Ф₃ как точка пересечения кривых Ф₁ = f₁(U_Mab) и суммарной кривой Ф₂ + Ф₃= f₄(U_Mab).

 

Рис. 3.9. Графическое решение режима в магнитной цепи с заданными м.д.с.

3.7. Примеры расчета разветвленных магнитных цепей