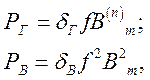Четырехполюсники. Электрические цепи с распределенными параметрами. Магнитные цепи. Магнитные цепи при периодических процессах, страница 14

                                                (4.2)

где δ_Г, δ_В – коэффициенты, зависящие от материала сердечника;

f – частота, Гц;

B_m – амплитуда магнитной индукции, Тл;

n – степень, зависящая от величины B_m.

Измерить можно только суммарные потери в стали Р_СТ. Для разделения потерь необходимо измерить суммарные потери на двух частотах при неизменной величине B_m.

Учет всех явлений усложняет исследование цепей с ферромагнитными элементами. Поэтому при расчетах принимают ряд допущений, упрощающих расчет и мало влияющих на характеристики рассматриваемого режима.

К расчету таких цепей широко применяется метод эквивалентных синусоид, при котором несинусоидальные токи, потоки, напряжения заменяют синусоидальными исходя из условия равенства действующих значений несинусоидальных и эквивалентных синусоидальных величин, из условия равенства потребляемой мощности.

Если одна из величин синусоидальна, то эквивалентную синусоиду, полученной для второй величины, ориентируют по фазе относительно первой.

Потери в стали вызывают отставание по фазе индукции В от напряженности Н. В комплексной форме для эквивалентных синусоид принимают , тогда , где δ – угол потерь, зависящий от величины потерь.

Применения метода эквивалентных синусоид позволяет проводить анализ цепей с ферромагнитными элементами с помощью векторных диаграмм.

В устройствах, где применяются материалы с узкой петлей гистерезиса, потерями в стали пренебрегают, принимая зависимость В(Н) однозначной. Это дает возможность получить однозначную зависимость Ф(i), что упрощает аналитический расчет по мгновенным значениям (метод аналитической аппроксимации, метод кусочно-линейной аппроксимации).

4.2 Катушка с ферромагнитным сердечником

Катушка с числом витков w намотана на стальной сердечник и подключена к источнику синусоидального напряжения (рис. 4.3).

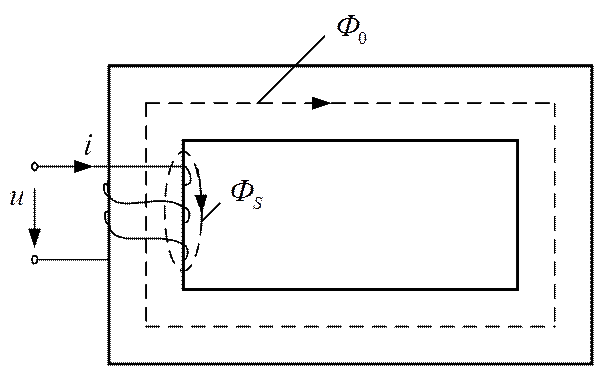
Рис. 4.3. Катушка с ферромагнитным сердечником

Ток катушки создает в сердечнике магнитный поток, большая часть которого замыкается по сердечнику и называется основным магнитным потоком Ф₀, меньшая часть замыкается по воздуху и называется потоком рассеяния Ф_S. Оба потока сцеплены со всеми витками катушки. Полное потокосцепление

                                             (4.3)

Уравнение, описывающие процесс в катушке, имеет вид:

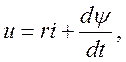                                                         (4.4)

где r – сопротивление обмотки.

Так как Ф_S замыкается по воздуху, магнитное сопротивление которого постоянно, то потокосцепление ψ_S линейно зависит от тока:

                                                          (4.5)

где    L_S – индуктивность рассеяния.

Уравнение (4.4) с учетом (4.3) и (4.5) преобразуется к виду:

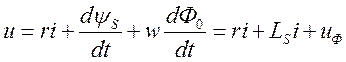                                      (4.6)

Уравнение (4.6) нелинейно, т. к. Ф₀ , а следовательно и u_Ф – нелинейно зависят от тока. При синусоидальном напряжении и ток i будет несинусоидальным.

Заменяя несинусоидальные кривые тока и потока эквивалентными синусоидами, запишем уравнение (4.6) в комплексной форме для действующих значений:

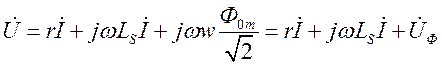                         (4.7)

Согласно уравнений (4.7) можно построить векторную диаграмму
(рис. 4.4). Построение начинаем с основного магнитного потока . ЭДС, наводимая в катушке основным потоком, равна  или 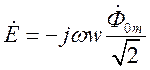 и  отстает по фазе от потока на угол . Напряжение  – опережает основной магнитный поток на угол .

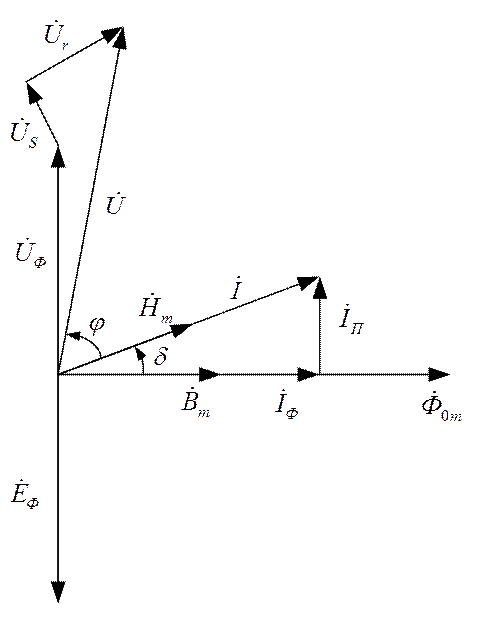
Рис. 4.4. Векторная диаграмма катушки с ферромагнитным сердечником

Магнитная индукция B_m в сердечнике совпадает по фазе с магнитным потоком, напряженность магнитного поля  за счет потерь в стали опережает индукцию на угол потерь δ.

Ток в катушке, определяемый законом полного тока для магнитной цепи, 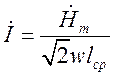, совпадает по фазе с напряженностью и имеет две составляющие: намагничивающий ток , совпадающий по фазе с основным магнитным потоком , и ток , совпадающий по фазе с напряжением  и определяемый потерями в стали:

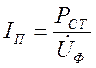                                                            (4.8)