Четырехполюсники. Электрические цепи с распределенными параметрами. Магнитные цепи. Магнитные цепи при периодических процессах, страница 2

1.4 Способы определения параметров четырехполюсника

Параметры четырехполюсника могут быть определены или расчетным путем по его внутренней схеме, или по результатам измерений с помощью измерительных приборов: вольтметра, амперметра, ваттметра или фазометра.

По известной внутренней схеме четырехполюсника его параметры можно определить различными способами:

а) составлением уравнений по законам Кирхгофа (либо методом контурных токов или узловых напряжений) и представлением их решения в виде одной из форм уравнений;

б) по значениям напряжений и токов в режимах холостого хода и короткого замыкания;

в) по входным сопротивлениям в режимах холостого хода и короткого замыкания;

г) разбивкой сложного четырехполюсника на более простые четырехполюсники, параметры которых известны.

П р и м е р 1. 1

Определить коэффициенты матрицы [А] для четырехполюсника (рис. 1.2) при заданных параметрах схемы: r = 60 Ом; ωL₁ = 20 Ом; ωL₂ = 60 Ом;
ωM = 10 Ом.

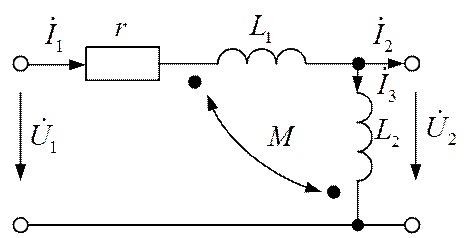
Рис. 1.2.

Из системы уравнений по законам Кирхгофа:

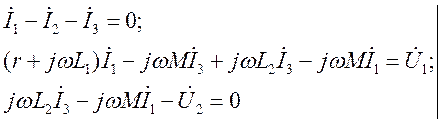                         (1.12)

исключением тока  и приведением (1.12) к виду (1.9) получим:

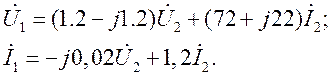
Следовательно,    .

П р и м е р 1. 2

Определить коэффициенты матрицы [А] двумя способами:

а) из уравнений Кирхгофа для режимов холостого хода и короткого замыкания;

б) через входные сопротивления холостого хода и короткого замыкания.

Параметры схемы: 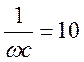 Ом,  Ом.

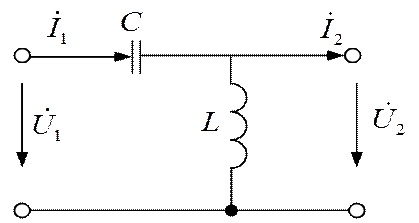
Рис. 1.3.

А. Из уравнений Кирхгофа для режимов холостого хода и короткого замыкания:

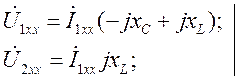,                                                   (1.13)

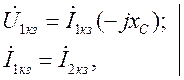,                                              (1.14)

получаем:

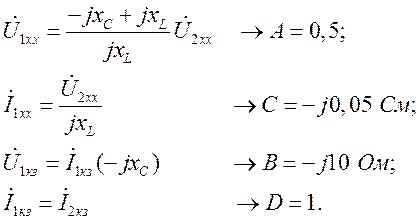
Б. Входные сопротивления холостого хода и короткого замыкания со стороны входных зажимов:

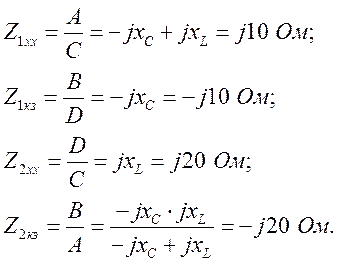
Выбирая три сопротивления из четырех и дополняя уравнением (1.10), находим

  

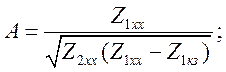
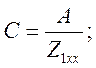
Получили матрицу .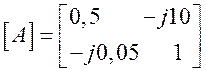

П р и м е р 1. 3

Для симметричного четырехполюсника в результате измерений получены значения сопротивлений: Z_xx=10 Ом; Z_кз=12,5 Ом.

Определить А – параметры четырехполюсника.

Для симметричного четырехполюсника

 

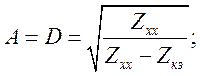
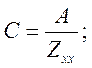
Получаем   

Следовательно, данным измерений соответствуют две матрицы:

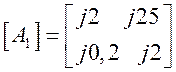 и 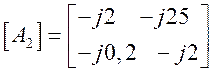                            (1.13)

и два эквивалентных четырехполюсника.

1.5. Схемы замещения четырехполюсника

Каждый пассивный четырехполюсник с известными параметрами одной из форм может быть представлен схемой замещения с минимальным числом элементов. Так как только три параметра четырехполюсника являются независимыми, то и минимальное число элементов в схеме замещения, отвечающих этим параметрам, равно трем. Такими простейшими схемами замещения являются Т – образная и П – образная (рис. 1.4).

               

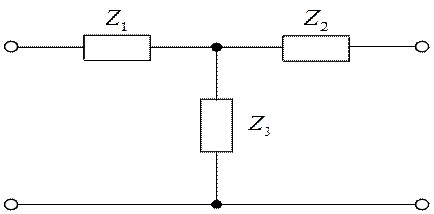
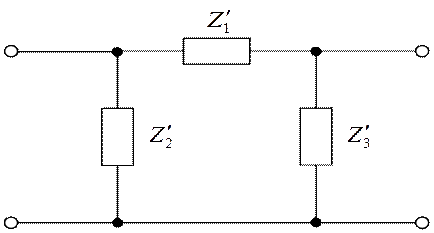
                    а                                                                         б

Рис. 1.4. а) Т – образная схема; б) П – образная схема

Матрица [А]_Т – для Т – образной схемы легко определяется из уравнений для контурных токов и имеет вид

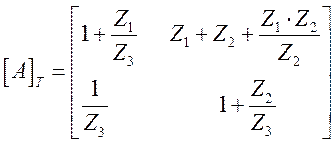.                                    (1.14)

Матрица [А]_П – для П – образной схемы находится из уравнений, составленных по методу узловых потенциалов и имеет вид:

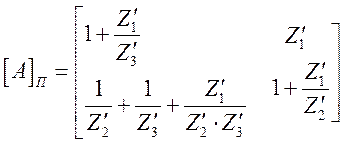.                                    (1.15)

Параметры схем замещения определяются через коэффициенты матриц [А]_Т и [А]_П :

– для Т – образной схемы:

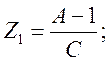
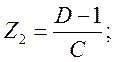
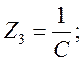                                     (1.16)

– для П – образной схемы:

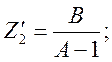
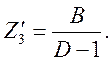                                     (1.17)

П р и м е р 1. 4

Определить параметры Т – образных схем замещения четырехполюсника по матрицам [А₁] и [А₂] примера 1.3.

Используя соотношения (1.16), находим параметры двух схем замещения, изображенных на рис. 1.5.

  

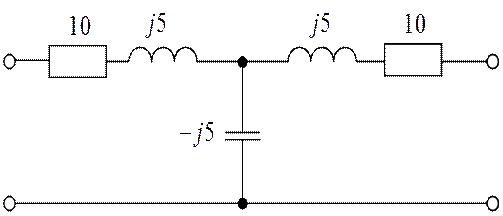
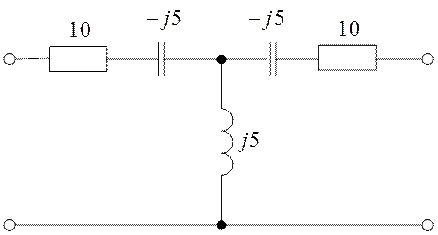
                     а                                                                         б

Рис. 1.5 Две эквивалентные схемы замещения

П р и м е р 1. 5

Для симметричного четырехполюсника известны А – параметры: А = D = 0,5 + j0,5; В = 20 + j 20 Ом; С = (-1,25 + j3,75)10^{-2 См. Определить параметры П – образной схемы замещения.}

Используя выражение (1.7), находим: