ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
РЯЗАНСКАЯ ГОСУДАРСТВЕННАЯ РАДИОТЕХНИЧЕСКАЯ АКАДЕМИЯ
В. С. ЛИТВИНОВА, Н. В. МЕЩЕРЯКОВ
CИНУСОИДАЛЬНЫЕ РЕЖИМЫ
В ОДНОРОДНЫХ ЛИНИЯХ
Часть I. Параметры. Уравнения. Режимы
 |
Рязань 2005
Федеральное агентство по образованию
Рязанская государственная радиотехническая академия
В. С. ЛИТВИНОВА, Н. В. МЕЩЕРЯКОВ
CИНУСОИДАЛЬНЫЕ РЕЖИМЫ
В ОДНОРОДНЫХ ЛИНИЯХ
Часть I. Параметры. Уравнения. Режимы
Учебное пособие
Рязань 2005
УДК 621.372.2
Синусоидальные режимы в однородных линиях. Часть I. Параметры. Уравнения. Режимы: Учеб. пособие / В. С. Литвинова, Н. В. Мещеряков; Рязан. гос. радиотехн. акад. Рязань, 2005. 24 с.
Рассматриваются параметры однородных линий и синусоидальные режимы в них. Приводятся основные характеристики и расчетные соотношения.
Предназначено студентам второго курса дневного отделения, изучающим дисциплины ²Основы теории цепей², ²Теоретические основы электротехники² и ²Электротехника и электроника².
Ил. 12.
Однородная линия, погонные параметры, волновое сопротивление, постоянная распространения линии, линия без потерь и без искажений, стоячие и бегущие волны
Печатается по решению редакционно-издательского совета Рязанской государственной радиотехнической академии.
Рецензент: кафедра теоретических основ электротехники РГРТА (зав. кафедрой А. П. Мишачев)
Л и т в и н о в а Варвара Сергеевна
М е щ е р я к о в Николай Владимирович
Синусоидальные режимы в однородных линиях
Редактор Е. В. Ипатова
Корректор С. В. Макушина
Подписано в печать Формат бумаги 60х84 1/16.
Бумага газетная. Печать трафаретная. Усл. печ. л. 1,5.
Уч. - изд. л. 1,5. Тираж 100 экз. Заказ
Рязанская государственная радиотехническая академия.
390005, Рязань, ул. Гагарина, 59/1.
Редакционно-издательский центр РГРТА.
© Рязанская государственная
радиотехническая академия, 2005
![]() 1.
Уравнения однородной линии. Погонные параметры
1.
Уравнения однородной линии. Погонные параметры
Однородная линия (рис. 1) является типичным примером электрической цепи с распределенными параметрами, в которой электрическое поле, магнитное поле и преобразование электромагнитной энергии в тепловую существуют вместе и изменяются во времени и пространстве.
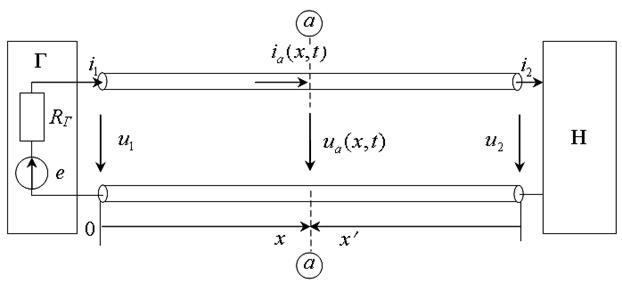 |
Рис. 1
Рассчитать режим в однородной линии в общем случае - значит получить ток и напряжение как функции двух переменных (координаты и времени) - ia (x, t), ua (x, t). Для этого требуется решить телеграфные уравнения (1) – систему дифференциальных уравнений в частных производных (см. прил. 1)

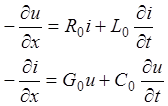 (1)
(1)
Сущность телеграфных уравнений состоит в том, что скорость убывания (знак ²-²) напряжения по линии в направлении распространения обусловлена продольными погонными параметрами R0, L0, а тока - поперечными G0, C0.
Погонными параметрами являются:
– Погонное активное сопротивление R0, Ом/м, - активное сопротивление прямого и обратного проводов отрезка линии длиной в 1 метр.
|
– Погонная активная проводимость G0, См/м, - активная проводимость между проводами за счет утечки из-за несовершенства изоляции отрезка линии длиной в 1 метр.
- Погонная емкость C0, Ф/м, - емкость между прямым и обратным проводами отрезка линии в 1 метр.
Линию называют однородной, если погонные параметры остаются неизменными по всей ее длине.
2. Расчетные соотношения и параметры однородной линии
в установившемся синусоидальном режиме
В результате расчета установившегося синусоидального
режима достаточно получить зависимости комплексов тока и напряжения от
координаты -![]() ,
,![]() . Поэтому сначала представим
телеграфные уравнения (1) в комплексной форме с учетом того, что синусоидальная
функция является мнимой частью вращающегося вектора
. Поэтому сначала представим
телеграфные уравнения (1) в комплексной форме с учетом того, что синусоидальная
функция является мнимой частью вращающегося вектора
|
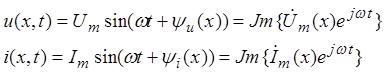 (2)
(2)
После подстановки (2) в (1) поменяем порядок операций дифференцирования и взятия мнимой части.
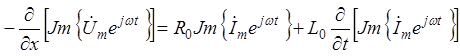 ®
®
![]()
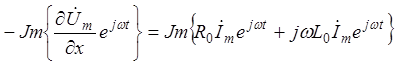
.
Так как мнимые составляющие вращающихся векторов в левой и правой частях уравнения равны, то равны и сами векторы
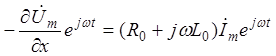 ®
® 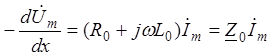 .
.
|

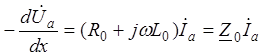
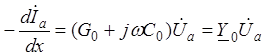
 где
где ![]() , Ом/м, и
, Ом/м, и ![]() , См/м - комплексные
погонные параметры линии
, См/м - комплексные
погонные параметры линии
![]()
|
![]()
Продифференцировав первое уравнение системы (4) и
подставив в него ![]() из второго, получим
из второго, получим 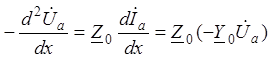 ®
®
 волновое
уравнение однородной линии
волновое
уравнение однородной линии 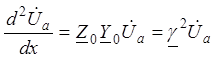 (5)
(5)
Корни соответствующего характеристического уравнения p2 = ![]() будут p1,2 = ±
будут p1,2 = ± ![]() и
поэтому решение волнового уравнения (5) для напряжения представляется в виде
двух волн
и
поэтому решение волнового уравнения (5) для напряжения представляется в виде
двух волн
![]() . (6)
. (6)

![]() Величину
Величину ![]() называют
постоянной распространения однородной линии
называют
постоянной распространения однородной линии
![]() (7)
(7)
Решение для тока получим из первого уравнения (3) и решения (6)
|
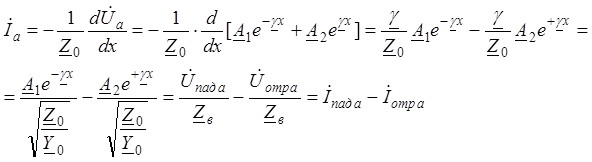
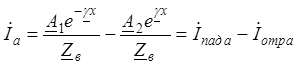 . (8)
. (8)
 Величину
Величину
![]() называют волновым сопротивлением
линии
называют волновым сопротивлением
линии
![]()
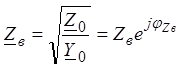 , Ом (9)
, Ом (9)
Для установления соотношения между величинами
отраженной и падающей волн вводят понятие коэффициента отражения от нагрузки
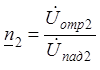 .
(10)
.
(10)
Из (6) и (8) выразим ![]() и
и
![]()
![]()
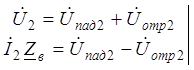
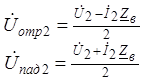
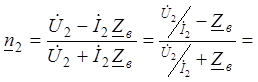

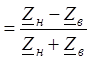 ®
® 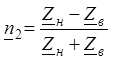 (11)
(11)
Выводы
1. Напряжение и ток в линии состоят из двух волн – падающей и отраженной (прямой и обратной). Знак ²-² у отраженной волны тока (8) объясняется тем, что положительное направление тока выбрано от генератора к нагрузке.
2. В волне (падающей или отраженной) напряжение и ток жестко связаны волновым сопротивлением (9) по закону Ома
![]()

|


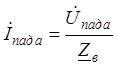
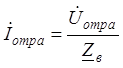
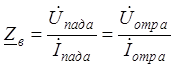 (12)
(12)
Заметим, что полные напряжение и ток связывает
не ![]() , а входное сопротивление линии
, а входное сопротивление линии
![]()
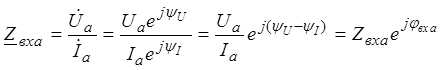 .
.
3. Режим в любом сечении линии (![]() ,
, ![]() )
рассчитывают по соотношениям (13), (14), полученным из решений (6), (8) путем
выражения постоянных интегрирования
)
рассчитывают по соотношениям (13), (14), полученным из решений (6), (8) путем
выражения постоянных интегрирования ![]() и
и
![]() через граничные условия:
через граничные условия:
![]() ,
, ![]() на
входе (x = 0) и
на
входе (x = 0) и ![]() ,
, ![]() на выходе (x¢ = 0).
на выходе (x¢ = 0).
![]()
![]() 3.1. x=0
3.1. x=0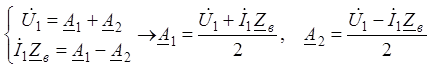 ®(6) и (8).
®(6) и (8).
|

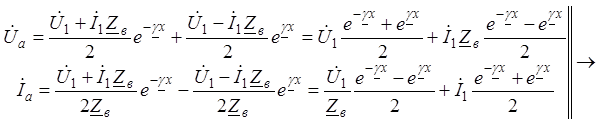
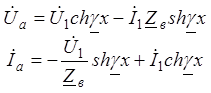 (13)
(13) Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.