Федеральное Агентство по Образованию
РГРТУ
Кафедра ТОЭ
Курсовая работа по ОТЦ:
«Режимы и характеристики электрических цепей с операционным усилителем»
Выполнил: ст. гр. 416
Бисмаркин Г. С.
Проверил:
Мещеряков Н. В.
Рязань 2006
Вариант №180
Задание:
1. Для заданной схемы найти передаточную функцию по напряжению H(p).
2. Используя полученную передаточную функцию записать выражения для H(jω), АЧХ и ФЧХ, построить карту нулей и полюсов. Провести расчёт и построить графики АЧХ и ФЧХ по карте нулей и полюсов.
3. Найти переходную и импульсную характеристики схемы и построить их графики.
4.
Построить график реакции схемы на
прямоугольный импульс напряжения амплитудой ![]() и
длительностью
и
длительностью ![]() .
.
1 шаг. Согласно заданию, необходимо рассчитать передаточную функцию H(p). Передаточной функцией называют отношение выходной величины к входной, выраженных в операторной или комплексной форме:
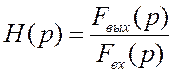
Искомой ПФ является коэффициент передачи напряжения на выход операционного усилителя:
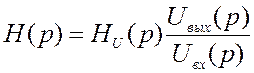
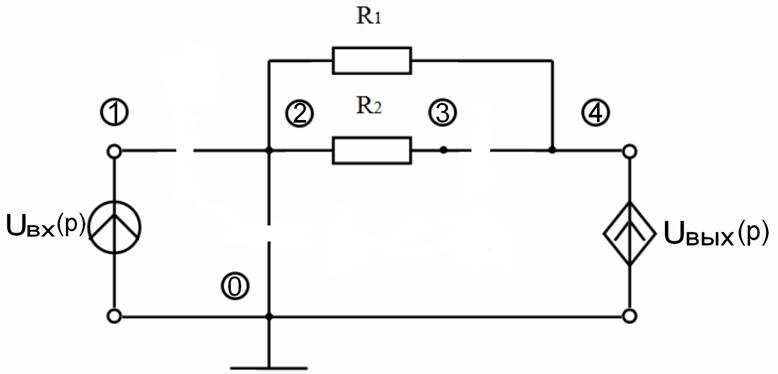
Схема электрическая принципиальная:
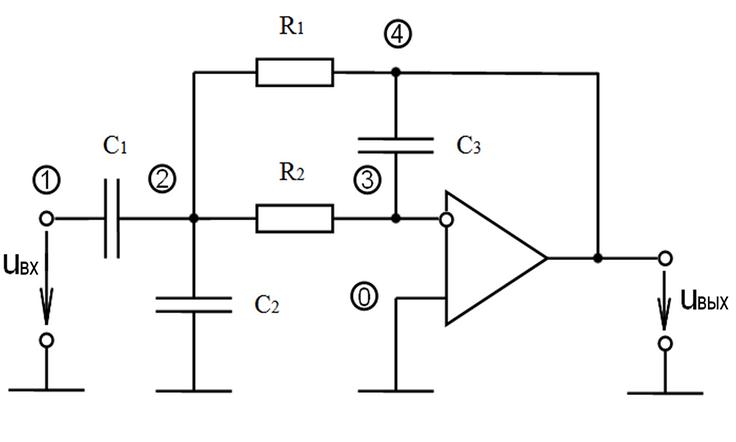
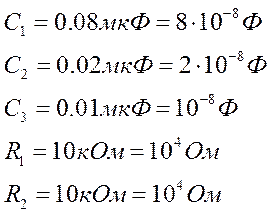
Особенности расчёта определяются наличием операционного усилителя.
ОУ обладает свойствами:
1. Входное сопротивление стремится к бесконечности.
2. Выходное сопротивление стремится к нулю, поэтому на выход можно поставить управляемый источник ЭДС.
3. Коэффициент усиления ОУ очень большой.
Поскольку напряжение на выходе конечно, а коэффициент усиления бесконечен, то
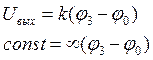
![]() – основное расчётное соотношение для цепей с ОУ
– основное расчётное соотношение для цепей с ОУ
Расчёт Н(р) сводится к расчёту
![]() через заданное
через заданное ![]()
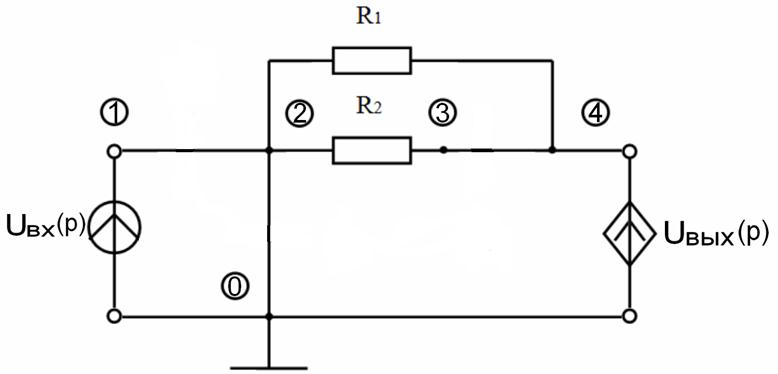
С учётом сказанного, расчётная схема примет вид:
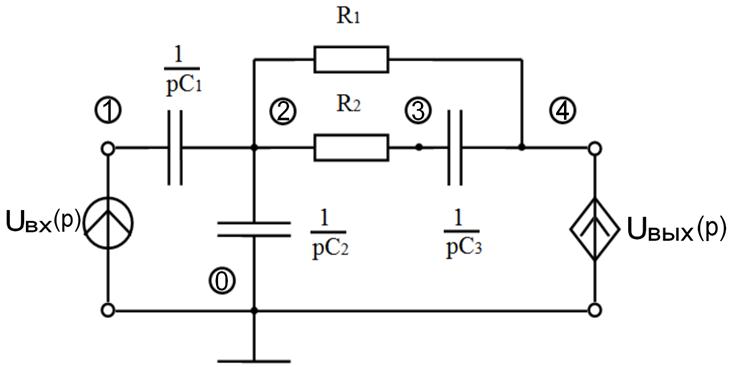
Основным расчётным соотношением для данной цепи является
φ3(p)=φ0(p)=0
Система уравнений по МУП:
φ1(p) = Uвх(p)
φ4(p) = Uвых(p)
φ3(p) = φ0(p)=0
φ2(p)(![]() +
+
![]() + pC2 + pC1) - φ1(p) pC1 - φ3(p)
+ pC2 + pC1) - φ1(p) pC1 - φ3(p) ![]() - φ4(p)
- φ4(p) ![]() = 0
= 0
φ3(p)(![]() +
pC3) - φ2(p)
+
pC3) - φ2(p) ![]() -
φ4(p) pC3 = 0
-
φ4(p) pC3 = 0
φ2(p)(2.10-4+p.10-7) – φ1(p)p8.10-8 – φ4(p)10-4 = 0
φ2(p) = - φ4(p)p10-4
H(p) = 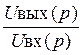 =
=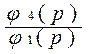 = - 8.103p/(p2 + 2000p +
107)
= - 8.103p/(p2 + 2000p +
107)
2 шаг. Расчёт частотных характеристик:
Комплексная частотная ПФ:
H(jω) =
H(p)|![]() =
= 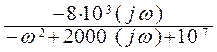 =
=
= 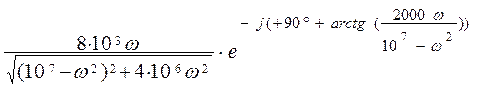 = H(ω)
= H(ω)![]()
АЧХ ПФ:
H(ω) = 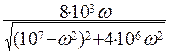
ФЧХ ПФ:
φн(ω) = 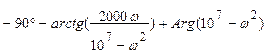
Графики частотных характеристик.
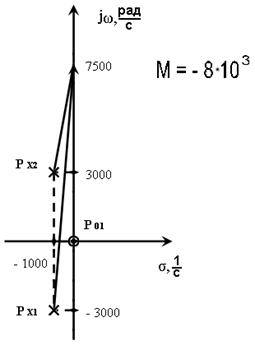
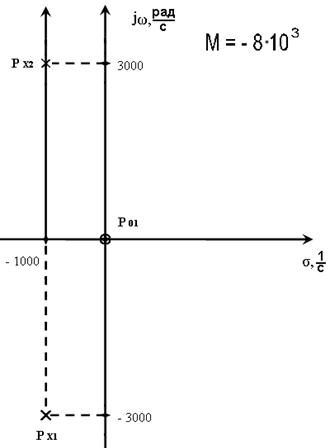
Построим ЧХ по карте передаточной функции. Картой ПФ является чертёж на комплексной плоскости, где отмечены нули, полюсы и масштабный коэффициент ПФ.
Нули:
F1(p) = - ![]() p
= 0
p
= 0
P01 = 0
Полюсы:
F2(p) = ![]() = 0
= 0
Px1,2 = α ± jωсв = -
1000 ± j3000 ![]()
Масштабный коэффициент:
М = - ![]()
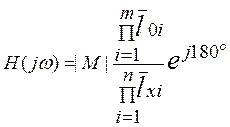
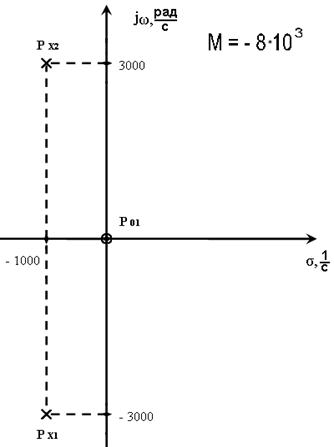
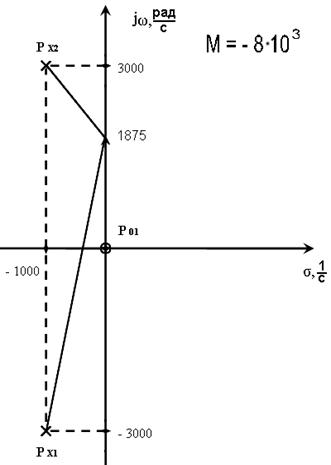
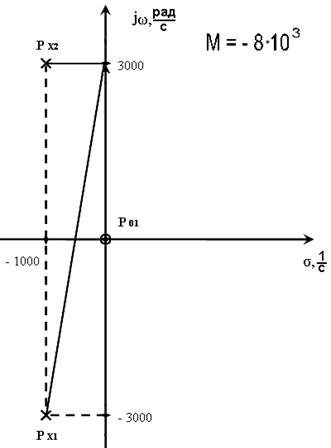
Отрезки l0i проведены из всех нулей в точку с заданной частотой jω. Векторы lxi - это отрезки, проведённые из всех полюсов в точку с заданной частотой.
1) 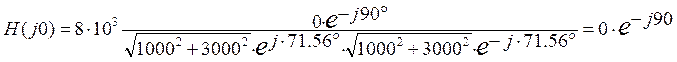
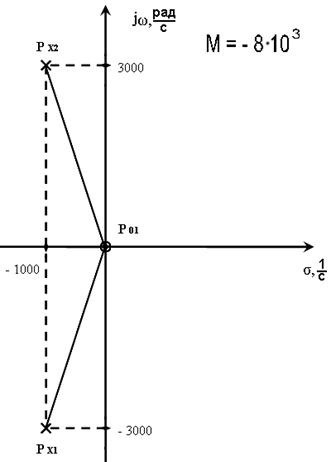
2) 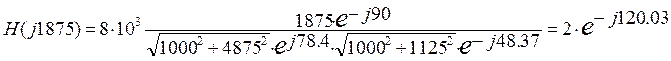
3) 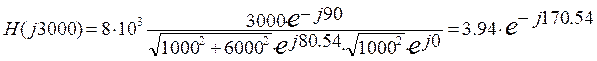
4) 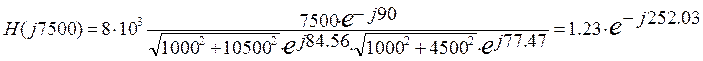
5) 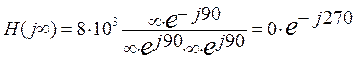
|
ω |
l01 |
lx1 |
lx2 |
φ01 |
φx1 |
φx2 |
H(ω) |
φ(ω) |
|
0 |
0 |
3162 |
3162 |
-90° |
71.56 |
-71.56 |
0 |
-90 |
|
1875 |
1875 |
4976.5 |
1505 |
-90° |
78.4 |
-48.37 |
2 |
-120.03 |
|
3000 |
3000 |
6000 |
1000 |
-90° |
80.54 |
0 |
3.94 |
-170.54 |
|
7500 |
7500 |
10547.5 |
4609.8 |
-90° |
84.56 |
77.47 |
1.23 |
-252.03 |
|
∞ |
∞ |
∞ |
∞ |
-90° |
90 |
90 |
0 |
-270 |
H(ω) = 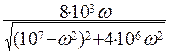
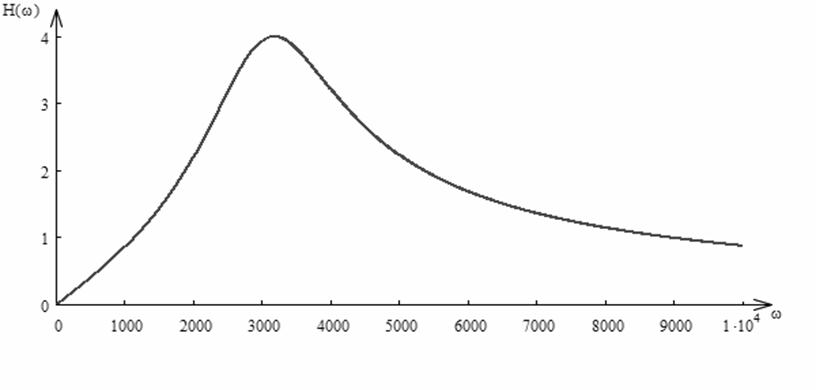
φн(ω) = 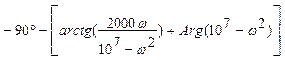
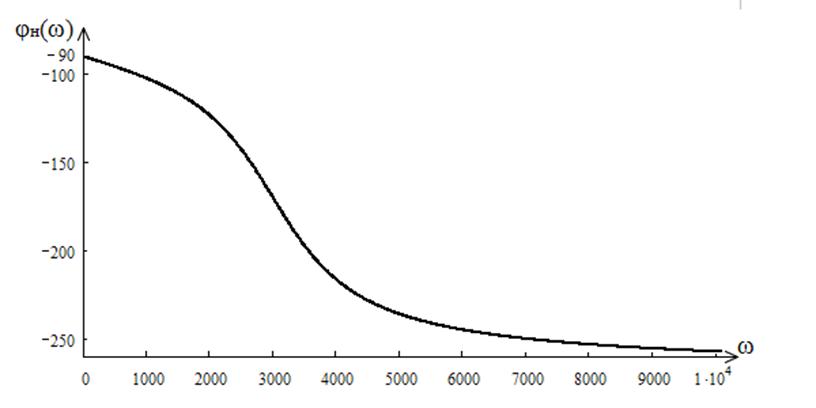
Проверка ПФ:
ω = 0
т.к. φ3(p) = φ0(p) = 0
по схеме: φ3(0) = φ2(0) = φ4(0) = Uвых(0) = 0
следовательно: Hсх(0) = 0 = Hрасч(0)
ω = ∞
т.к. φ3(p) = φ0(p) = 0
по схеме: φ3(∞) = φ2(∞) = φ4(∞) = Uвых(∞) = 0
следовательно: Hсх(∞) = 0 = Hрасч(∞)
Вывод: ПФ расчётная соответствует ПФ по схеме, следовательно, расчёты верны.
3 шаг. Временные характеристики.
Импульсная характеристика.
g(t) ![]() H(p) = F1(px1)/F2 (px1)
H(p) = F1(px1)/F2 (px1)
g(t) = 2A1e-αtcos(ωсвt + ![]() 1),
A1=F1(px1)/F2
(px1)
1),
A1=F1(px1)/F2
(px1)
A1=- 8.103( -1000 - j3000)/(2.( - 1000 – j3000) + 2000) = - 4216.37e – j18.44
g(t) = - 8432.74e-1000tcos(3000t – 18.44)
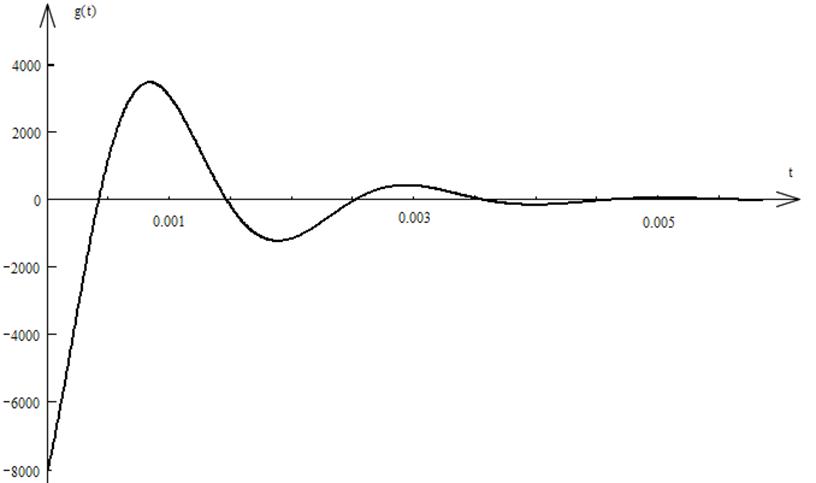
Переходная характеристика.
h(t) ![]() H(p) /p= F1(px1)/F2 (px1)
H(p) /p= F1(px1)/F2 (px1)
h(t) = 2A1e-αtcos(ωсвt + ![]() 1),
A1= F1(px1)/F2
(px1)
1),
A1= F1(px1)/F2
(px1)
A1=- 8.103/(2.( - 1000 – j3000) + 2000) = 4/3e – j90
h(t) = 8/3e-1000tcos(3000t – 90) = - 8/3e-1000tsin(3000t)
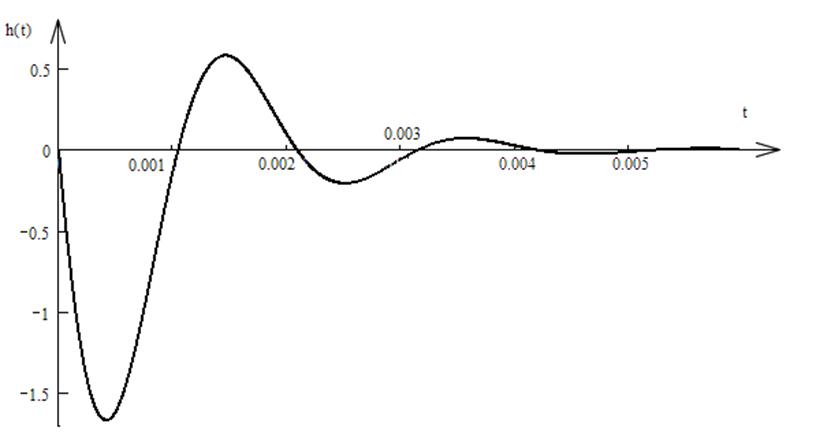
Проверка ПХ:
![]() =
=
= - 8/3e0sin(0)
![]() – 8/3.(- 1000e-1000tsin(3000t) +
3000e-1000tcos(3000t)) =
– 8/3.(- 1000e-1000tsin(3000t) +
3000e-1000tcos(3000t)) =
= - 8432.74e-1000tcos(3000t – 18.44)
Вывод: импульсная характеристика найденная по обобщенной производной соответствует расчётной импульсной характеристике, следовательно, расчёты верны.
Проверка соответствия H(p) и h(t):
H(0) = - 8000.0/(02 + 2000.0 + 107) = 0 = h(∞) = - 8/3e-∞sin(∞) = 0
H(∞) = - 8000. ∞/(∞2 + 2000. ∞ + 107) = 0 = h(0) = - 8/3e-0sin(0) = 0
Вывод: H(p) соответствует h(t), следовательно, расчёты верны.
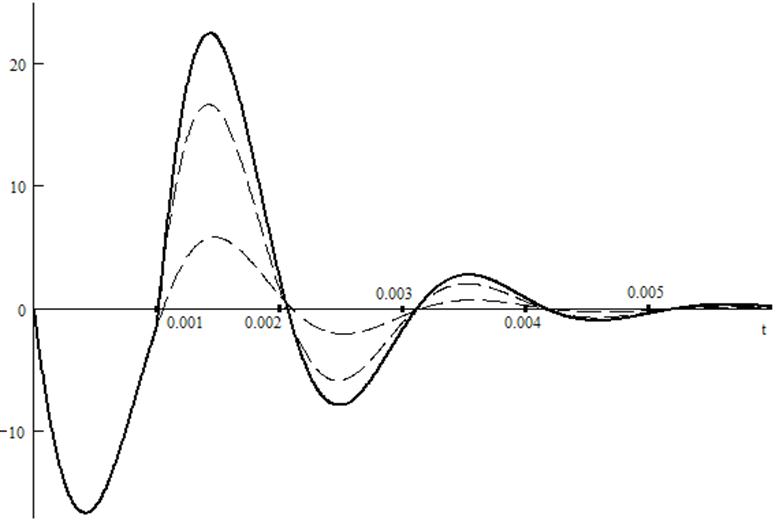
4 шаг. Расчёт реакции на прямоугольный импульс.
![]() ,
, ![]() .
.
Представим П-импульс как сумму двух ступенек:
![]()

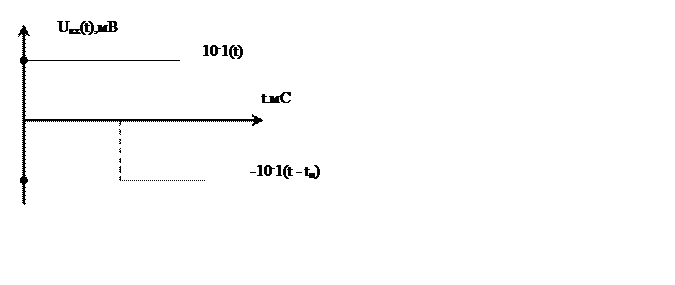
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.