3753
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
РЯЗАНСКАЯ ГОСУДАРСТВЕННАЯ РАДИОТЕХНИЧЕСКАЯ АКАДЕМИЯ
ОСНОВЫ ТЕОРИИ ЦЕПЕЙ
АНАЛИЗ УСТАНОВИВШИХСЯ И ПЕРЕХОДНЫХ ПРОЦЕССОВ
Методические указания
Рязань 2005
УДК 621.3.01
Основы теории цепей. Анализ
установившихся и переходных процессов: Методические указания / Рязан. гос.
радиотехн. акад.; Сост. В.П. Рынин, М.А. Суслова, С.М. Милюков, В.И. Ивашкин,
В.Н. Зуб; Под ред. В.П. Рынина. Рязань, 2005. 16 с.
Содержат набор задач и методические материалы, необходимые для выполнения курсовой работы, расчетно-графических работ, а также указания к самостоятельной работе по курсам ОТЦ и «Общая электротехника».
Предназначены для студентов дневного
отделения специальностей
1905, 1906, 1909, 2010, 2012.
Ил. 3.
Ветвь, контур, закон Кирхгофа, потенциал, постоянный ток, синусоидальный ток, мгновенное значение тока, модуль, фаза, постоянная времени, переходная характеристика.
Печатается по решению методического совета Рязанской государственной радиотехнической академии.
Рецензент: кафедра теоретических основ электротехники РГРТА
(зав. кафедрой доц. А.П. Мишачев)
МЕТОДЫ АНАЛИЗА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
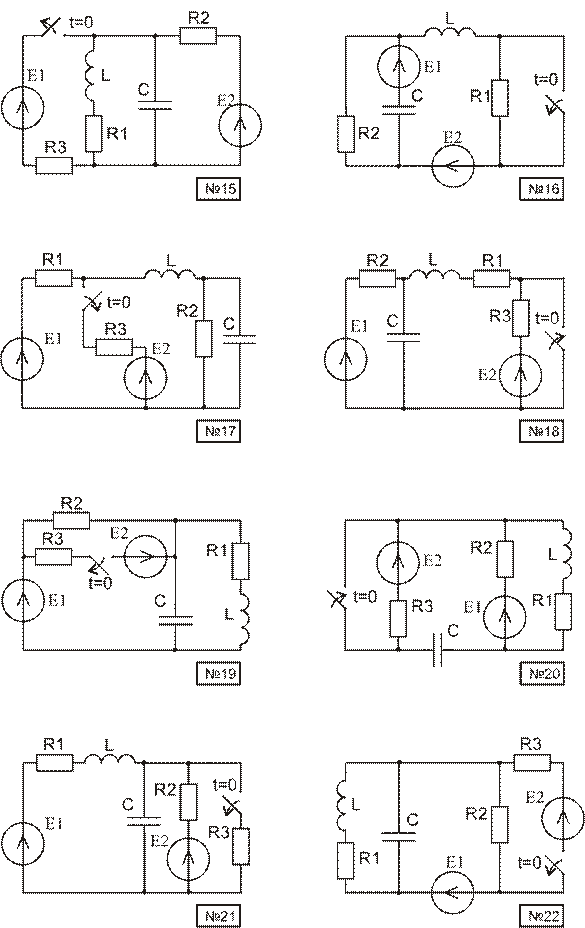
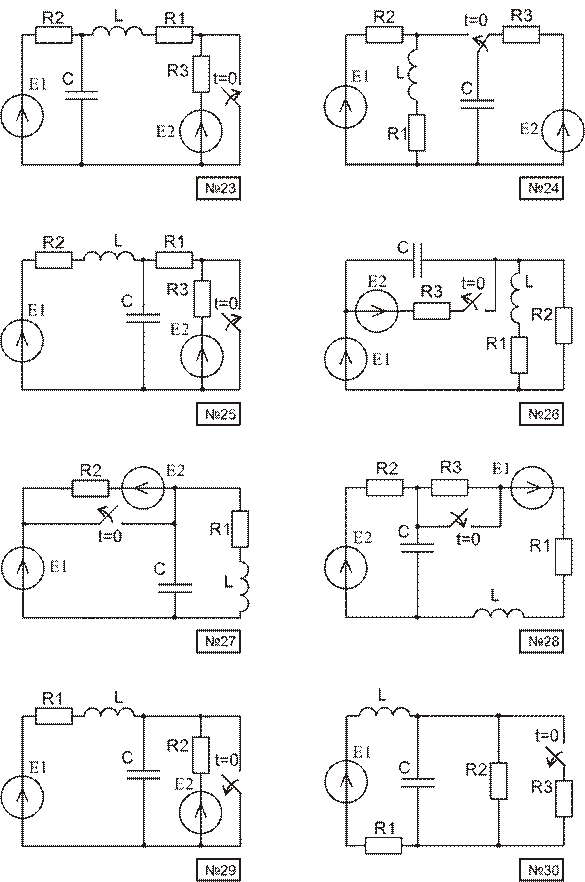
Используя материал приложения А, начертить расчетную схему. Номер схемы равен порядковому номеру, под которым фамилия студента записана в журнале группы. Номер варианта параметров элементов схемы и пункты задания, подлежащие выполнению, указываются преподавателем.
1. Найти токи во всех ветвях схемы на основе уравнений, составленных по законам Кирхгофа.
2. Найти токи во всех ветвях схемы методом узловых потенциалов.
3. Найти токи во всех ветвях схемы методом контурных токов.
4. Рассчитать ток в одной из ветвей методом эквивалентного генератора.
РАСЧЕТ УСТАНОВИВШИХСЯ РЕЖИМОВ В ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА
Используя материал приложения Б,
начертить расчетную схему. Номер схемы равен порядковому номеру, под которым
фамилия студента записана в журнале группы. Номер варианта параметров элементов
схемы и пункты задания, подлежащие выполнению, указываются преподавателем. Для
всех вариантов угловая частота
ω =
1000 рад-1.
1. Найти комплексные токи во всех ветвях схемы. Записать выражения для мгновенных значений токов.
2. Построить потенциальную диаграмму и векторную для токов.
3. Найти комплексную, активную и реактивную мощности на всех источниках и всех пассивных элементах электрической цепи.
РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ
В ЛИНЕЙНЫХ ЦЕПЯХ
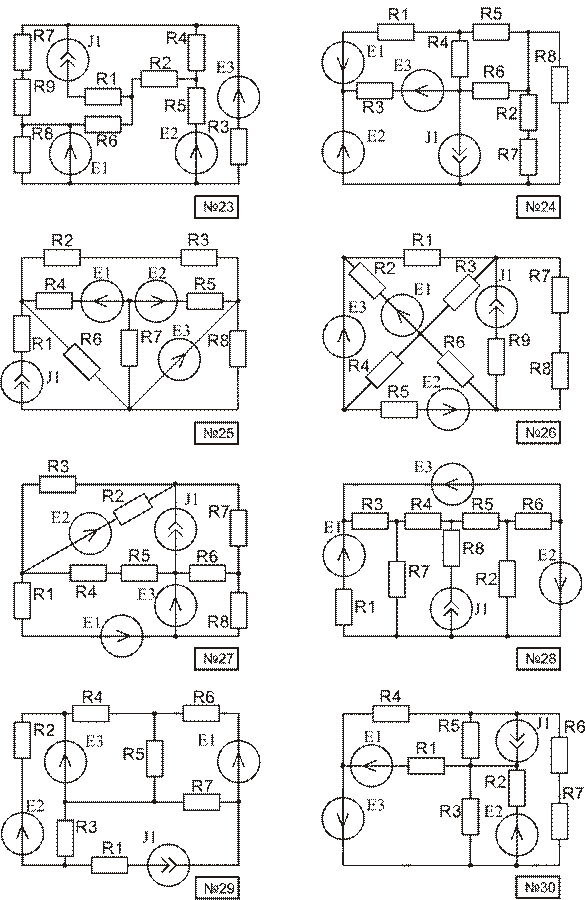
Используя материал приложения В, начертить расчетную схему. Номер схемы равен порядковому номеру, под которым фамилия студента записана в журнале группы. Номер варианта параметров элементов схемы и пункты задания, подлежащие выполнению, указываются преподавателем.
1. Рассчитать ток в одной из ветвей классическим методом.
2. Рассчитать ток в одной из ветвей операторным методом.
3. Построить график рассчитанного тока.
4. В схеме, получающейся после коммутаций, оставить один источник напряжения по указанию преподавателя. Остальные приравнять к нулю. Рассчитать переходную характеристику, считая воздействием напряжение на зажимах цепи, подключенной к источнику напряжения, а реакцией – ток в ветви или напряжение на элементе, указанные преподавателем. Построить рассчитанную переходную характеристику h(t).
Пример расчета переходной характеристики.
Для схемы № 8 приложения В после коммутации получаем схему, приведенную на рис. 1.
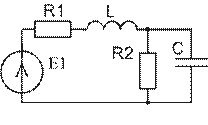 Параметры
элементов схемы:
Параметры
элементов схемы:
R1=0 Ом; R2=R=500 Ом;
L=0,02 Гн; С=1 мкФ.
|
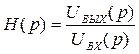 .
.
Операторная схема для расчета Н(р) приведена на рис.2. Для указанной схемы
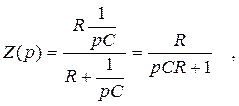
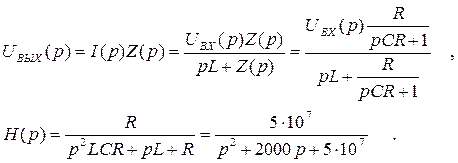
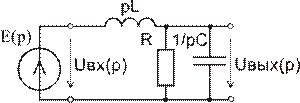
|
Переходная характеристика h(t) является оригиналом функции
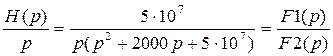 .
.
Для нахождения h(t) воспользуемся теоремой разложения.
Для этого найдем корни
знаменателя F2(p)=0, р(р2 +2000р+5∙107 )=0,
р1=0 и р2,3= -1000±7000j c-1 . В соответствии с найденными корнями записываем
решение для h(t) в виде
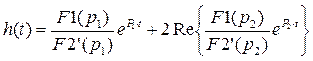 , где F1(р1)= F1(р2)=
5∙107.
, где F1(р1)= F1(р2)=
5∙107.
Найдем
производную знаменателя F2′(p)=3p2+4000p+5∙107,
F2′( р1)= 5∙107,
F2′( р2)=3 (-1000+j7000)2+4000
(-1000+j7000)+ 5∙107= -99∙106еj8º .
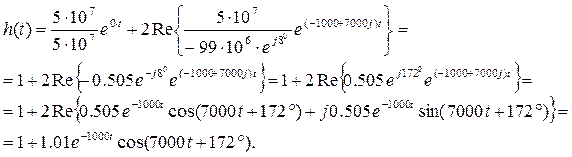 График
функции h(t) приведен рис.3.
График
функции h(t) приведен рис.3.
|
|

Рис. 3
Приложение А
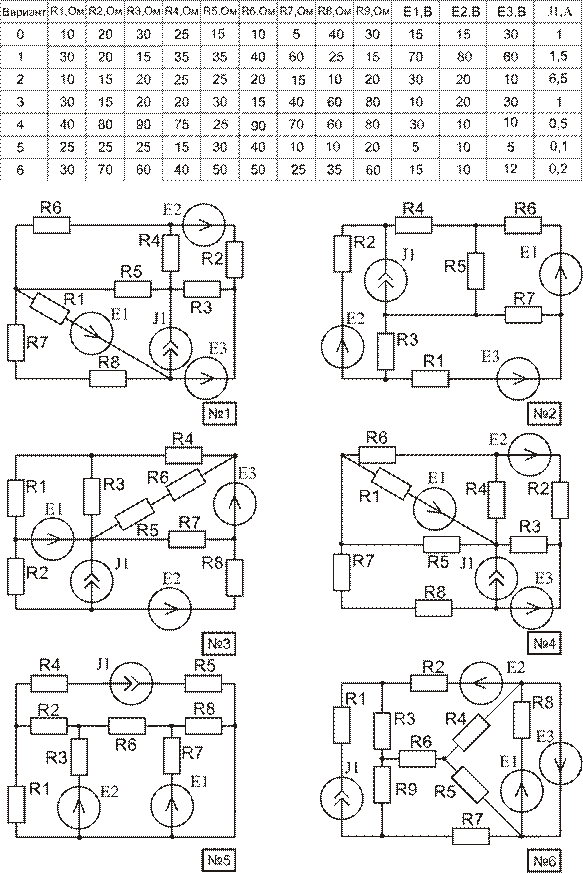
Приложение А (продолжение)

Приложение А (продолжение)
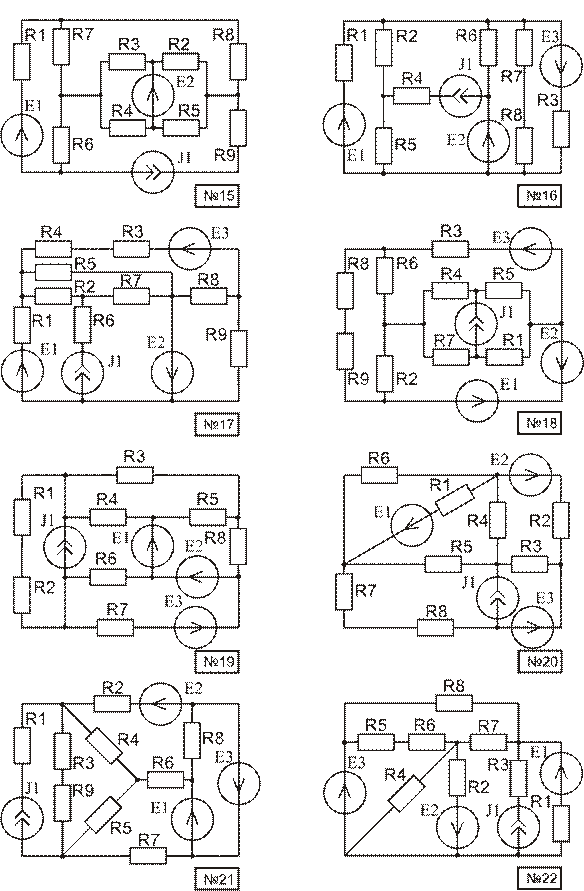
Приложение А (окончание)
Приложение Б
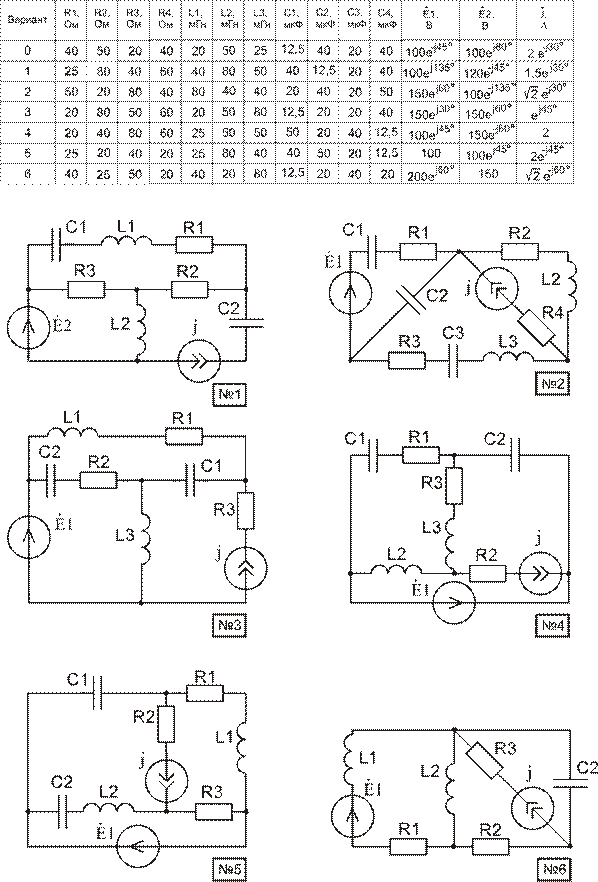
Приложение Б (продолжение)
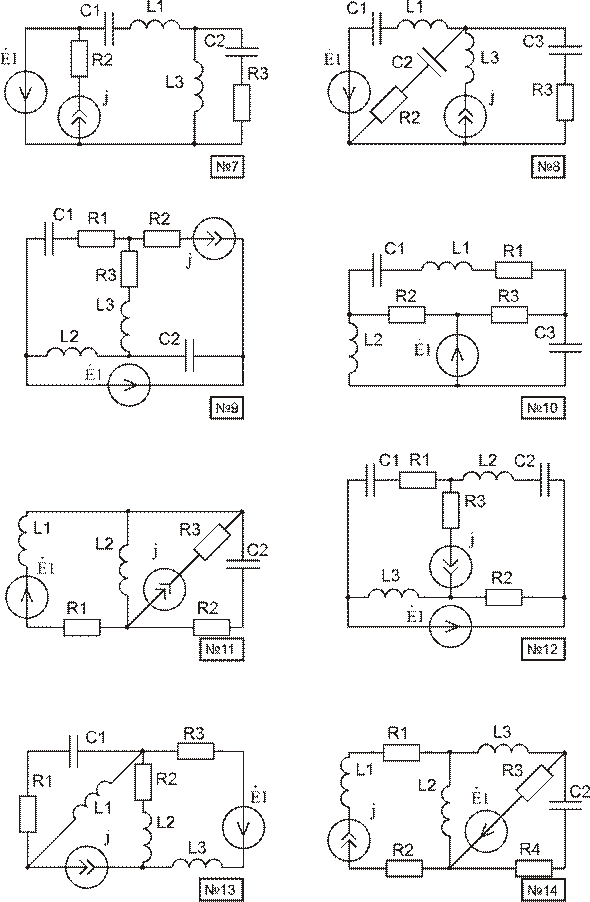
Приложение Б (продолжение)

Приложение Б (окончание)
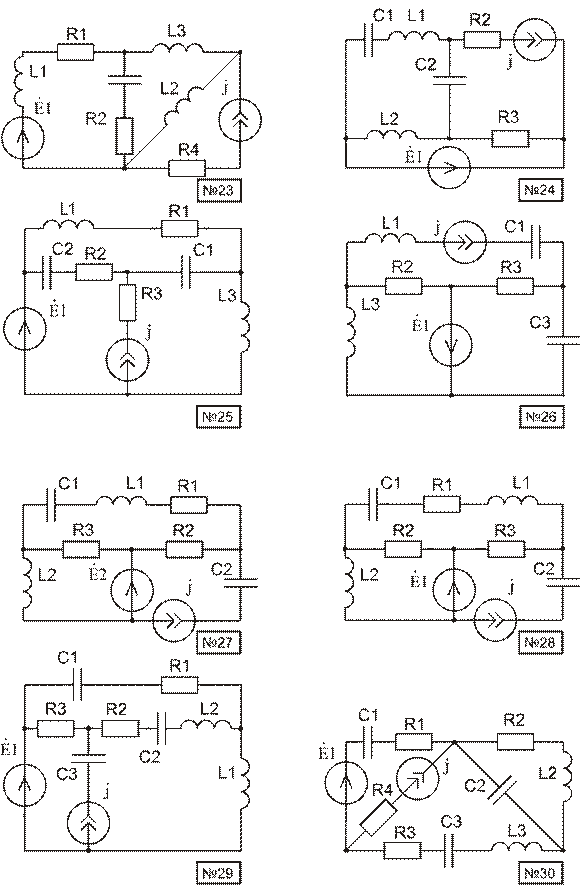
Приложение В
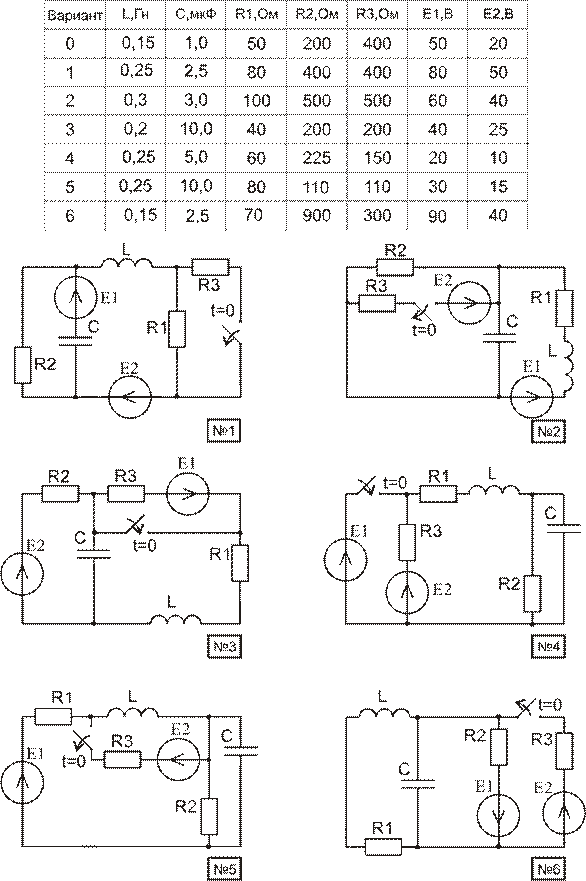
Приложение В (продолжение)
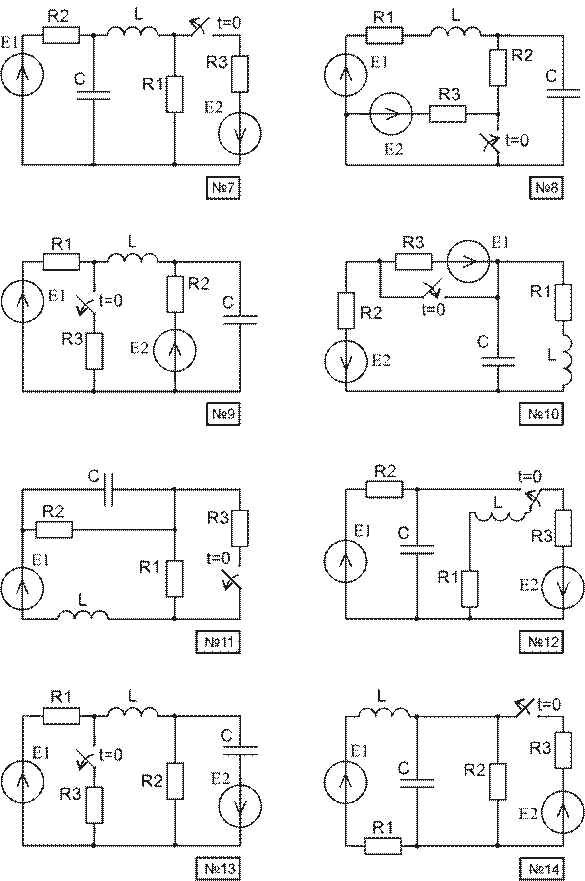
Приложение В (продолжение)
Приложение В (окончание)
Основы теории цепей
Анализ установившихся и переходных процессов
Составители: Р ы н и н Владимир Петрович
С у с л о в а Маргарита Александровна
М и л ю к о в Сергей Михайлович
И в а ш к и н Валерий Иванович
З у б Владимир Николаевич
Редактор Р. К. Мангутова
Корректор С. В. Макушина
Подписано в печать 08.08.05. Формат бумаги 60 х 84 1/16.
Бумага газетная. Печать трафаретная. Усл.печ.л. 1,0.
Уч.-изд.л. 1,0. Тираж 100 экз. Заказ .
Рязанская государственная радиотехническая академия.
390005, Рязань, ул. Гагарина, 59/1.
Редакционно-издательский центр РГРТА.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.