Электротехника \ Основы теории цепей

Синусоидальные режимы в однородных линиях. Часть II. Расчет режимов по номограммам: Учебное пособие

Страницы работы

23 страницы (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

РЯЗАНСКАЯ ГОСУДАРСТВЕННАЯ РАДИОТЕХНИЧЕСКАЯ АКАДЕМИЯ

В. С. ЛИТВИНОВА, Н. В. МЕЩЕРЯКОВ

CИНУСОИДАЛЬНЫЕ РЕЖИМЫ

В ОДНОРОДНЫХ ЛИНИЯХ

Часть II. Расчет режимов по номограммам

Рязань 2005

Федеральное агенство по образованию

Рязанская государственная радиотехническая академия

В. С. ЛИТВИНОВА, Н. В. МЕЩЕРЯКОВ

CИНУСОИДАЛЬНЫЕ РЕЖИМЫ

В ОДНОРОДНЫХ ЛИНИЯХ

Часть II. Расчет режимов по номограммам

Учебное пособие

Рязань 2005

УДК 621.372.2

Синусоидальные режимы в однородных линиях. Часть II. Расчет режимов по номограммам: Учеб. пособие / В. С. Литвинова, Н. В. Мещеряков; Рязан. гос. радиотехн. акад. Рязань, 2005. 36 с.

Рассматриваются вывод, описание диаграммы Вольперта и ее применение для измерения комплекса сопротивления нагрузки, согласования и расчета режимов. Приводятся соответствующие примеры расчетов.

Предназначено для студентов второго курса дневного отделения, изучающих дисциплины ²Основы теории цепей², ²Теоретические основы электротехники², ²Электротехника и электроника².

Ил. 26. Библиограф.: 3 назв.

Диаграмма Вольперта, коэффициент отражения, относительное сопротивление, стоячие и бегущие волны, узел и пучность напряжения, коэффициент бегущей волны, согласование линии с нагрузкой.

Печатается по решению редакционно-издательского совета Рязанской государственной радиотехнической академии.

Рецензент: кафедра теоретических основ электротехники РГРТА (зав. кафедрой А. П. Мишачев)

Л и т в и н о в а Варвара Сергеевна

М е щ е р я к о в Николай Владимирович

Синусоидальные режимы в однородных линиях

Редактор Р. К. Мангутова

Корректор С. В. Макушина

Подписано в печать 29. 07. 05 . Формат бумаги 60х84 1/16.

Бумага газетная. Печать трафаретная. Усл. печ. л. 2,25.

Уч. - изд. л. 2,25. Тираж 100 экз. Заказ

Рязанская государственная радиотехническая академия.

390005, Рязань, ул. Гагарина, 59/1.

Редакционно-издательский центр РГРТА.

радиотехническая академия, 2005

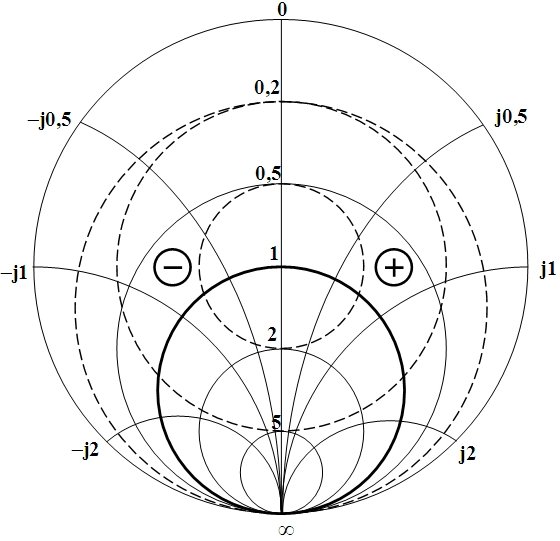
В технике высоких частот для выполнения расчётов широко используется диаграмма А. Р. Вольперта (именуемая в дальнейшем ДВ).

ДВ представляет собой рисунок на комплексной плоскости, в пределах которого размещены три семейства окружностей постоянных:

§ коэффициента бегущих волн ,

§ относительного (нормированного) активного сопротивления линии ,

§ относительного (нормированного) реактивного сопротивления линии .

ДВ позволяет рассчитать:

o входное сопротивление линии,

o распределение действующих напряжения и тока вдоль линии,

o параметры согласующих устройств.

В основу структуры ДВ положены зависимости нормированных напряжения, тока и сопротивления от координаты при различных коэффициентах отражения.

1. Представление режима в линии через коэффициент отражения. Диаграмма Вольперта

1.1. Коэффициент отражения. Семейство окружностей постоянного

Коэффициентом отражения (КО) от нагрузки называют отношение отраженной волны к падающей в конце линии

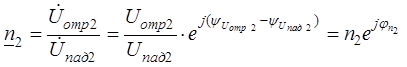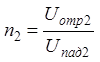– модуль КО, – аргумент КО

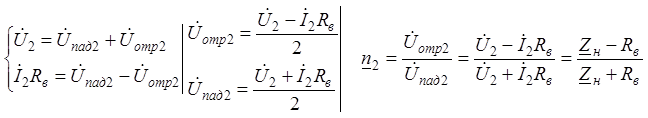Выразим через и из соотношений в нагрузке

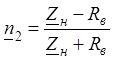(1)

Из выражения (1) следует, что КО зависит от нагрузки и соотношения между и волновым сопротивлением.

1. При (КЗ), (ХХ) и чисто реактивной нагрузке () коэффициент отражения от нагрузки , т.е. волна от нагрузки отражается полностью и в линии устанавливается режим чисто стоячих волн.

2. При согласованной нагрузке () коэффициент отражения n₂ = 0, отраженной волны нет и в линии устанавливается режим чисто бегущих волн.

3. При произвольной нагрузке () коэффициент отражения 0<n₂ <1 и в линии устанавливается режим смешанных волн.

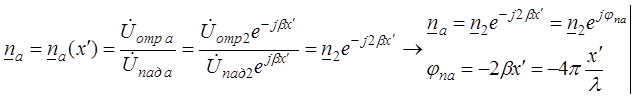Введём понятие коэффициента отражения в произвольно взятом сечении линии а–а как отношение отраженной волны к падающей в этом сечении (рис. 1):

(2)

Заметим, что в произвольном сечении никаких неоднородностей нет, отражения не возникает и означает лишь наличие в этом сечении падающей и отраженной волн.

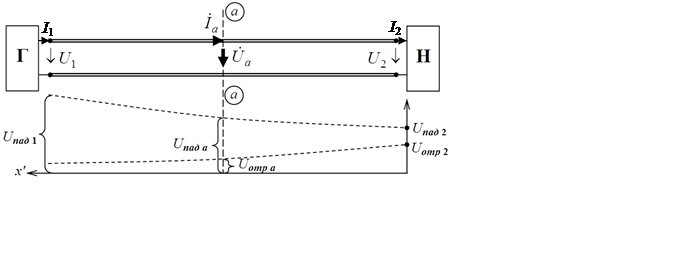
Рис. 1

Выразим напряжение и ток в произвольном сечении a-а с учетом (2).

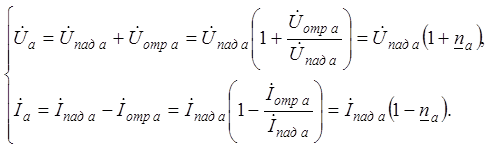
Относительные (нормированные) напряжение и ток

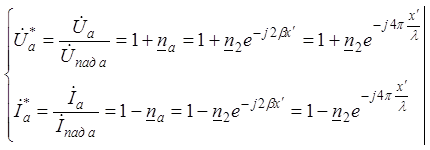(3)

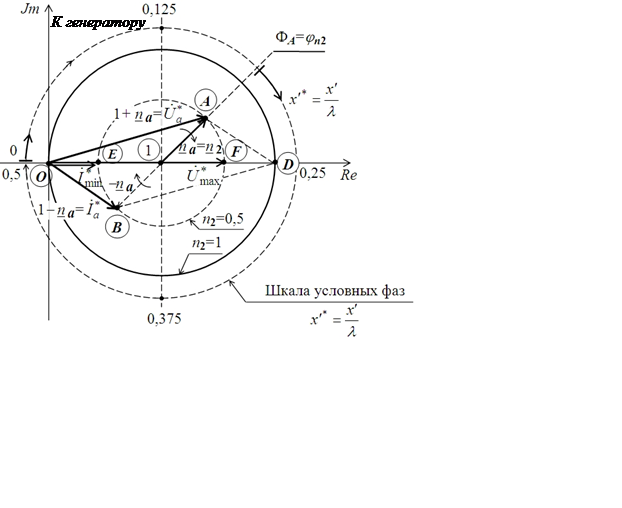на комплексной плоскости представляются векторами (рис. 2), концы которых (точки А и В) описывают окружность радиусом , двигаясь по ходу часовой стрелки по мере роста , т.е. при перемещении по линии передачи от нагрузки к генератору.

Рис. 2

Вектор 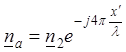совершает полный оборот (360º) при прохождении по линии расстояния, равного 0,5:

Половине оборота (180º) вектора n_а соответствует перемещение по линии на 0,25.

Заметим, что U^*_max = 1 + n₂ = OF, U^*_min = 1 - n₂ = OE.

Для привязки конкретных значений к конкретной координате х¢ вводится шкала условных фаз – шкала относительных длин линии 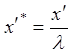, т.е. в долях длины волны. Если, например, точке А (рис. 2) соответствует конец линии передачи (положение вектора ), то отсчитывается от условной фазы Ф_А= в направлении часовой стрелки.

Из сказанного следует вывод о том, что геометрическим местом концов векторов 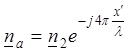является семейство концентрических окружностей радиусом n₂ с равномерным шагом от 0 до 1 (рис. 3).

На практике чаще вместо КО применяют коэффициент бегущей волны .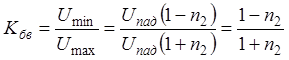

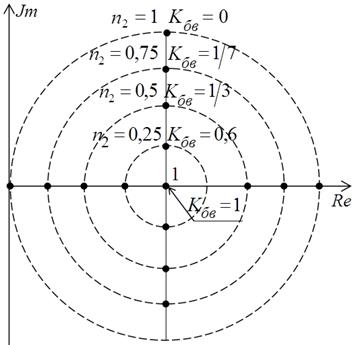Поэтому окружности постоянного n₂ градуируют

в соответствующих значе-

ниях К_бв. При этом:

- внешней окружности соответствует n₂ = 1 и К_бв = 0,

- центру диаграммы – n₂ = 0 и К_бв= 1 (точка полного согласования),

Рис. 3

- коэффициенту отражения n₂=0,5 соответствует

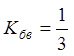и т. д.

Выводы

1. Линиями постоянного К_бв являются концентрические окружности с переменным шагом.

2. Движению по окружности постоянного К_бв на диаграмме по ходу часовой стрелки на условную фазу 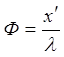соответствует перемещение по физической линии передачи в сторону генератора на расстояние и наоборот.