Положение вектора ![]() (рис.
2) позволяет получить функции распределения по координате
(рис.
2) позволяет получить функции распределения по координате ![]() относительных (нормированных)
напряжения
относительных (нормированных)
напряжения ![]() и тока
и тока ![]() .
.
При определённых значениях ![]() вектор
вектор ![]() совпадает
с положительным направлением вещественной оси и напряжение оказывается
максимальным,
совпадает
с положительным направлением вещественной оси и напряжение оказывается
максимальным, ![]() (отрезок OF), а ток – минимальным,
(отрезок OF), а ток – минимальным, ![]() (отрезок OE), и совпадающим по фазе с напряжением. В этом сечении
наблюдаются пучность напряжения и узел тока.
(отрезок OE), и совпадающим по фазе с напряжением. В этом сечении
наблюдаются пучность напряжения и узел тока.
Через половину оборота, т.
е. через ![]() , вектор
, вектор ![]() займёт
противоположное направление, напряжение станет минимальным,
займёт
противоположное направление, напряжение станет минимальным, ![]() (отрезок OE), а ток – максимальным,
(отрезок OE), а ток – максимальным, ![]() (отрезок
OF). Они вновь совпадут по фазе. В этом
сечении наблюдаются узел напряжения и пучность тока.
(отрезок
OF). Они вновь совпадут по фазе. В этом
сечении наблюдаются узел напряжения и пучность тока.
По относительным
величинам ![]() и
и ![]() (рис.
4) для соответствующих значений
(рис.
4) для соответствующих значений ![]() можно построить
графики распределения абсолютных значений
можно построить
графики распределения абсолютных значений ![]() ,
используя масштабные коэффициенты
,
используя масштабные коэффициенты ![]() ,
, ![]() и связь
и связь ![]() .
.
Учитывая, что в линии без потерь падающая волна не
затухает (![]() ),
),
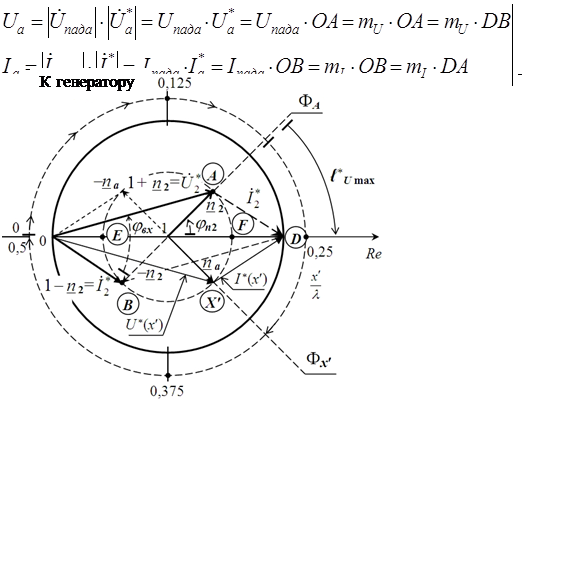 |
Рис. 4
Масштабные коэффициенты ![]() ,
, ![]() проще
получить по граничным условиям: U1, I1 – на входе линии, U2, I2 – на выходе. Например, если точке А
(рис. 4) соответствует положение вектора
проще
получить по граничным условиям: U1, I1 – на входе линии, U2, I2 – на выходе. Например, если точке А
(рис. 4) соответствует положение вектора ![]() ,
то отрезку ОА соответствует напряжение на нагрузке
,
то отрезку ОА соответствует напряжение на нагрузке ![]() ,
отрезку OB= DА соответствует ток в нагрузке
,
отрезку OB= DА соответствует ток в нагрузке ![]() . Поэтому при
известных граничных условиях U2, I2
. Поэтому при
известных граничных условиях U2, I2

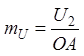

![]() Абсолютные напряжение и ток вычисляют по длинам отрезков
Абсолютные напряжение и ток вычисляют по длинам отрезков ![]() и
и ![]()
![]()
![]() , где
, где ![]() - текущая точка на окружности Кбв.
- текущая точка на окружности Кбв.
Положение точки Х ¢ на окружности Кбв (радиусом n2) получают как точку пересечения с
этой окружностью луча, проведенного из центра на фазу ![]() на
шкале условных фаз.
на
шкале условных фаз.
Для построения графиков U(x¢) и I(x¢) сначала определяют масштабы mU, mI, отмечают на графиках максимальные и минимальные значения: Umax = mU × OF, Umin = mU × OE, Imax = mI × DE, Imin = mI × DF. Затем находят координату ближайшей к нагрузке особой точки (пучности или узла напряжения). Согласно рис. 4 ближайшей от нагрузки особой точкой является пучность напряжения с координатой
ℓU max= ℓ*U max × l = (ФF - ФА) ×l .
Далее на линии через 0,25l отмечают узел напряжения. Для вычисления промежуточных точек между пучностью и узлом отрезок линии в 0,25l и условную фазу в 0,25 на ДВ разбивают на равное число частей, проводят лучи из центра в соответствующие точки на шкале условных фаз. По точкам пересечения лучей с Кбв получают длины отрезков ОХ¢ и DХ¢, соответствующие значениям U(x¢) и I(x¢).
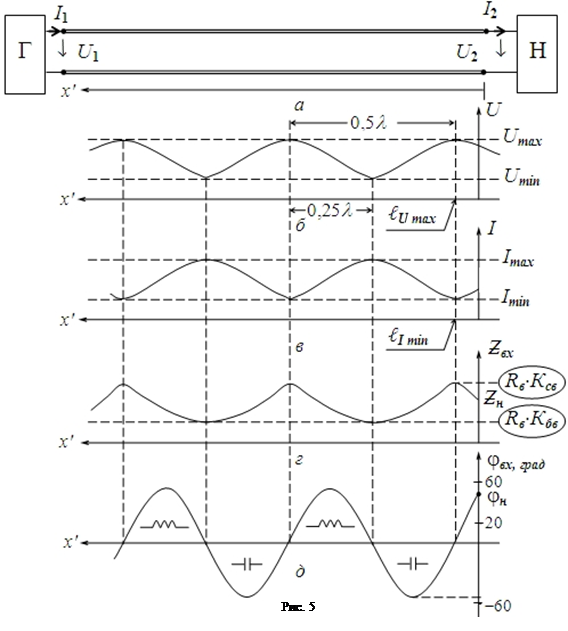
Далее на графиках через каждую четверть волны картина зеркально повторяется (рис. 5).
 |
Выводы
1. С помощью номограммы линий Кбв (рис. 2, 4) по длинам отрезков можно рассчитать распределение действующих значений напряжения и тока вдоль линии на основе граничных условий.
Заметим, что на линии пучностям напряжения соответствуют узлы тока, а узлам напряжения – пучности тока.
2. По
измеренным отрезкам ![]() и
и ![]() для
конкретных координат х¢
(рис. 4) можно установить зависимость комплекса входного сопротивления линии
(рис. 5)
для
конкретных координат х¢
(рис. 4) можно установить зависимость комплекса входного сопротивления линии
(рис. 5)
![]()
![]()
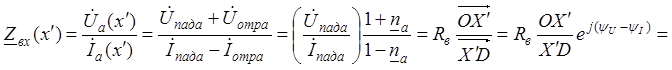
![]() , где
, где 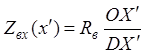 –
модуль, а
–
модуль, а ![]() – аргумент входного сопротивления.
– аргумент входного сопротивления.
Заметим, что через каждую четверть длины волны периодически сменяется характер входного сопротивления линии. В узлах и пучностях входное сопротивление чисто активно:
 |
 |
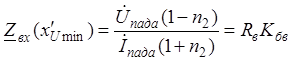
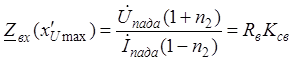 .
.
Максимальный
сдвиг по фазе в ![]() между
между ![]() и
и ![]() наблюдается
в режиме чисто стоячих волн (n2 = 1, Кбв = 0). В согласованном режиме
наблюдается
в режиме чисто стоячих волн (n2 = 1, Кбв = 0). В согласованном режиме ![]() напряжение и ток совпадают по фазе в
любой точке линии.
напряжение и ток совпадают по фазе в
любой точке линии.
1.3. Семейства линий постоянных активного и реактивного сопротивлений однородной линии
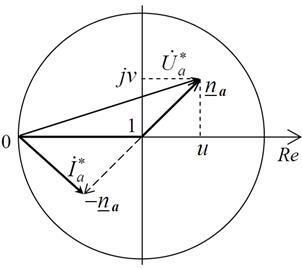 Выясним закономерности
расположения нормированных активной и реактивной составляющих входного
сопротивления линии на комплексной плоскости (рис. 6).
Выясним закономерности
расположения нормированных активной и реактивной составляющих входного
сопротивления линии на комплексной плоскости (рис. 6).
|
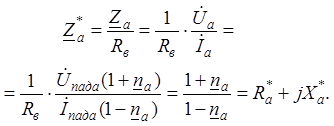 Получим
выражения активного
Получим
выражения активного 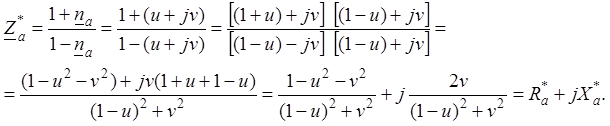

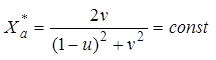

|
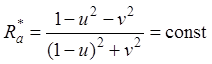 и
и
![]()
|
![]()
Обе части равенства ![]() умножим на
умножим на ![]() и
приведем подобные:
и
приведем подобные:
![]() ®
®![]() .
.
Разделим последнее выражение на ![]() и добавим в его левую и правую части
слагаемое
и добавим в его левую и правую части
слагаемое 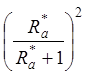 :
:

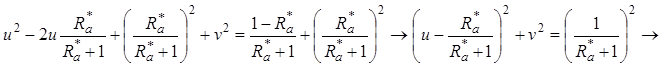
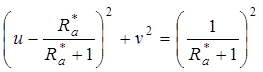 - уравнение окружности.
- уравнение окружности.
 Радиус
-
Радиус
- 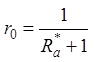 .
.![]() Смещение центра:
Смещение центра:
![]()
 по вещественной оси
по вещественной оси 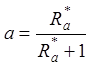 , по мнимой оси
, по мнимой оси ![]() ,
т. е. центры окружностей располагаются на вещественной оси в системе координат
,
т. е. центры окружностей располагаются на вещественной оси в системе координат ![]() (рис. 7).
(рис. 7).
|

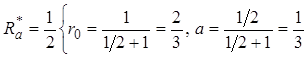 1.
1. 2.
3. 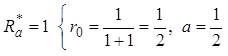 .
.
4.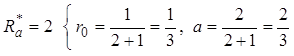 .
.
5. ![]() .
.
Рис. 7
Выводы
1.
Все окружности семейства ![]() имеют общую точку с координатой
(2,0).
имеют общую точку с координатой
(2,0).
2.
Внешней окружности соответствует ![]() , т.е. нулевое активное
сопротивление.
, т.е. нулевое активное
сопротивление.
3.
Окружность ![]() вырождается
в точку с координатой (2,0).
вырождается
в точку с координатой (2,0).
Обе части равенства 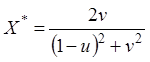 умножим на
умножим на ![]() , поделим на
, поделим на ![]() и
дополним до полного квадрата
и
дополним до полного квадрата

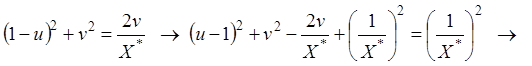
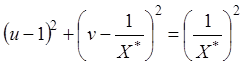 - уравнение
окружности.
- уравнение
окружности.
![]()
 Радиус
Радиус 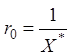 .
.
Смещение центра: по вещественной оси
![]() ,
,
 по мнимой оси
по мнимой оси 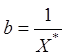 .
.
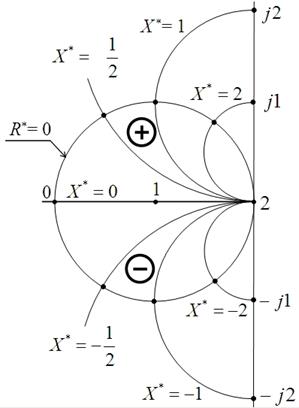
Построим ряд окружностей (рис. 8).
 1.
1. 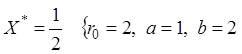 .
.
2. ![]() .
.
3. 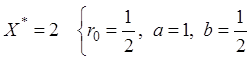 .
.
4. ![]() .
.
5. ![]() .
.
Выводы
1. Семейство окружностей Х *=const
находится внутри окружности R*=0, т.к. за её пределами R*< 0, т.е. не существует. Поэтому окружность R* = 0 есть
![]() геометрическое
место чисто реактивных сопротивлений. Рис.
8
геометрическое
место чисто реактивных сопротивлений. Рис.
8
2. Все окружности семейства Х *=const касаются вещественной оси в точке (2,0). В верхней части комплексной плоскости X *> 0, в нижней X *< 0. Вещественная ось (как окружность X *= 0 с бесконечным радиусом и смещением) разделяет положительные и отрицательные реактивности.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.