3.
Определение ![]() по ДB.
по ДB.
3.1.
Отмечают на ДB точку В - входное
сопротивление в узле напряжения ![]() на вертикальном
диаметре с условной фазой ΦВ=0.
на вертикальном
диаметре с условной фазой ΦВ=0.
3.2.
На шкале условных фаз от фазы ΦВ=0 в сторону опорной точки
откладывают относительное смещение минимума 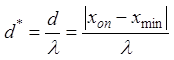 и
отмечают условную фазу входного сопротивления линии в опорной точке
и
отмечают условную фазу входного сопротивления линии в опорной точке ![]() .
.
Если опорная точка xопотносительно точки xmin оказалась со стороны генератора, то следует двигаться по шкале условных фаз к генератору. Если опорная точка xоп относительно xmin оказалась со стороны нагрузки, то следует двигаться к нагрузке.
3.3. Проводят луч, соединяющий центр ДB с условной фазой ![]() . В точке пересечения луча с
окружностью Кбв находится искомая величина
. В точке пересечения луча с
окружностью Кбв находится искомая величина ![]() .
.
Абсолютное значение сопротивления нагрузки ![]() .
.
Рассмотрим пример измерения сопротивления нагрузки Zн.
С целью измерения сопротивления нагрузки в линии с волновым сопротивлением Rв=300 Ом с помощью измерительной линии получены результаты:
- в режиме КЗ нулевые показатели индикатора напряжения наблюдались напротив значений х1=5 см, х2=35 см, х3=65 см на метрической шкале. Точку с координатой х2 будем считать опорной. xоп=х2=35 см;
![]()
![]() - в нагрузочном режиме ближайший
минимум (узел) напряжения относительно опорной точки (х2=35 см)
оказался в точке xmin=44,6 см. Показания индикатора
в узле min=2,4 деления, в пучности max=15 делений;
- в нагрузочном режиме ближайший
минимум (узел) напряжения относительно опорной точки (х2=35 см)
оказался в точке xmin=44,6 см. Показания индикатора
в узле min=2,4 деления, в пучности max=15 делений;
- направление отсчёта координаты по метрической шкале совпадает с направлением движения от генератора к нагрузке.
Требуется по полученным результатам найти Zн.
Решение
Для наглядности представим результаты эксперимента схематично (рис. 13).
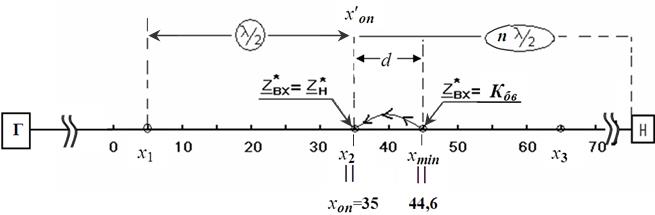
Рис. 13
1. За опорную точку принята координата х2=xоп=35 см. В ней входное сопротивление равно
искомой величине ![]() .
.
2. Длина волны ![]() .
.
|
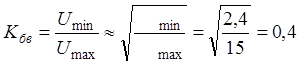
4. Входное сопротивление линии в сечении xmin чисто активно и равно Кбв ![]() .
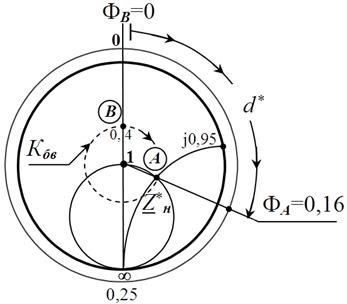
На ДB (рис. 14) это сопротивление отмечено точкой В
с нулевой фазой (ФВ=0).
.
На ДB (рис. 14) это сопротивление отмечено точкой В
с нулевой фазой (ФВ=0).
 5. Смещение минимума напряжения относительно опорной
точки произошло в сторону нагрузки на расстояние
5. Смещение минимума напряжения относительно опорной
точки произошло в сторону нагрузки на расстояние
|
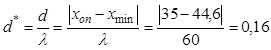 Следовательно , для
Следовательно , для
определения
![]() необходимо перейти от точки В
в опорную точку (т. А), т. е. в сторону генератора на расстояние
необходимо перейти от точки В
в опорную точку (т. А), т. е. в сторону генератора на расстояние ![]() .
.
Рис. 14 6. Условная фаза в опорной точке ФА= ФВ + d *= 0 + d * = d * = 0,16 отмечена на шкале и в нее проведён луч.
7. Искомая величина Zн находится в точке пересечения луча с Кбв=0,4 (т. А)
![]() Ом.
Ом.
2.2. Расчёт режима в нагруженной линии
По заданным условиям рассматривают два вида задач.
1.
На входе линии задан источник с эквивалентными э.д.с. ![]() и
внутренним сопротивлением RГ. Требуется получить режим на входе и выходе при
известной нагрузке.
и
внутренним сопротивлением RГ. Требуется получить режим на входе и выходе при
известной нагрузке.
2.
Задано требуемое напряжение на выходе (U2)
при известной нагрузке ![]() . Надо найти режим на входе
линии (U1, I1, P1).
. Надо найти режим на входе
линии (U1, I1, P1).
Задача 1
Пусть на входе линии (ℓ
= 163,8 см, Rв= 100
Ом, uф= 2,5·108 м/с) действует источник ![]() В с внутренним сопротивлением
RГ = 100 Ом, нагрузка
комплексная (Rн=20 Ом,
В с внутренним сопротивлением
RГ = 100 Ом, нагрузка
комплексная (Rн=20 Ом, 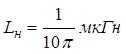 , рис. 15).
, рис. 15).
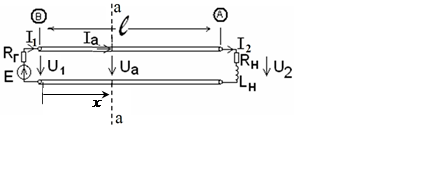 Требуется рассчитать режим в нагрузке (U2, I2, P2) и построить график распределения
действующих значений напряжений U(x) и тока I(x)
вдоль линии.
Требуется рассчитать режим в нагрузке (U2, I2, P2) и построить график распределения
действующих значений напряжений U(x) и тока I(x)
вдоль линии.
|
||||
Решение
Поскольку задан источник, то следует рассчитать сначала режим на входе линии. При этом необходимо узнать ее входное сопротивление Zвх1 .
1-й шаг. Расчёт входного сопротивления линии
Его можно рассчитать по формуле или определить по ДB.
![]() Для обращения к ДB
требуются величины: длина волны
Для обращения к ДB
требуются величины: длина волны 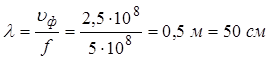 , комплекс
сопротивления нагрузки
, комплекс
сопротивления нагрузки
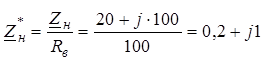
|
Кбв=0,1 определяется концентрической окружностью через точку А.
Условная фаза нагрузки получается на месте пересечения шкалы условных фаз с лучом через точку А : Фн = ФА = 0,126.
Условная фаза входного сопротивления линии получается дополнением к условной фазе нагрузки относительной длины линии без целого числа полуволн:
![]() Отметим на шкале условную фазу ФВ = 0,402 и проведём луч в центр
диаграммы (рис. 16). В точке пересечения этого луча с Кбв=0,1 получим нормированное
сопротивление
Отметим на шкале условную фазу ФВ = 0,402 и проведём луч в центр
диаграммы (рис. 16). В точке пересечения этого луча с Кбв=0,1 получим нормированное
сопротивление ![]() .
.
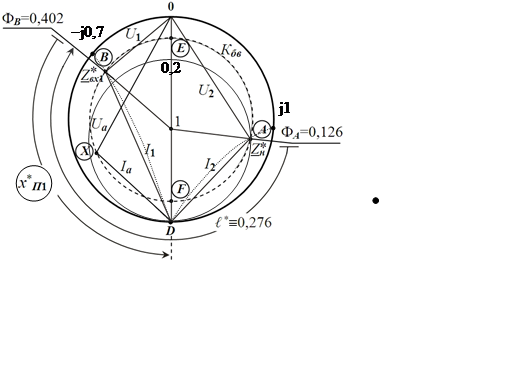 |
Рис. 16
- Входное сопротивление линии в
абсолютных единицах ![]() Ом.
Ом.
2-й шаг. Режим на входе линии
Ток 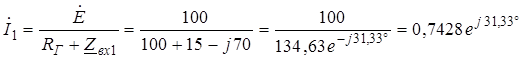 А.
А.
![]() Напряжение
Напряжение 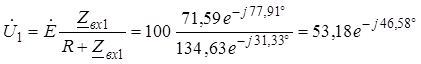 В.
В.
Активная мощность .
Масштабы напряжения и тока через граничные условия на входе (U1, I1) получим делением полученных значений U1 и I1 на соответствующие отрезки на ДB:
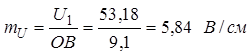 ,
, 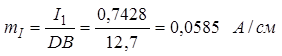 .
.
3-й шаг. Режим в нагрузке
![]() ,
, ![]()
![]() .
.
Проверка по двум критериям:
|
![]() 2)
2)
позволяет сделать вывод, что расчёты выполнены с допустимой погрешностью (не более 5 %).
![]()
![]() 4-й шаг. Графики распределения действующих
значений U(x) и I(x) получим через отрезки OX и DХ (рис. 16)
4-й шаг. Графики распределения действующих
значений U(x) и I(x) получим через отрезки OX и DХ (рис. 16)
![]()
![]()
Определим сначала минимальные и максимальные значения напряжения и тока
![]()
![]()
![]()
![]()
![]()
![]()
Отметим на графиках значения U1, I1 и U2, I2 (рис. 17).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.