Синусоидальные режимы в однородных линиях. Часть II. Расчет режимов по номограммам: Учебное пособие, страница 3

3. Окружность X ^*= ¥ вырождается в точку с координатой (2,0).

1.4. Описание диаграммы Вольперта

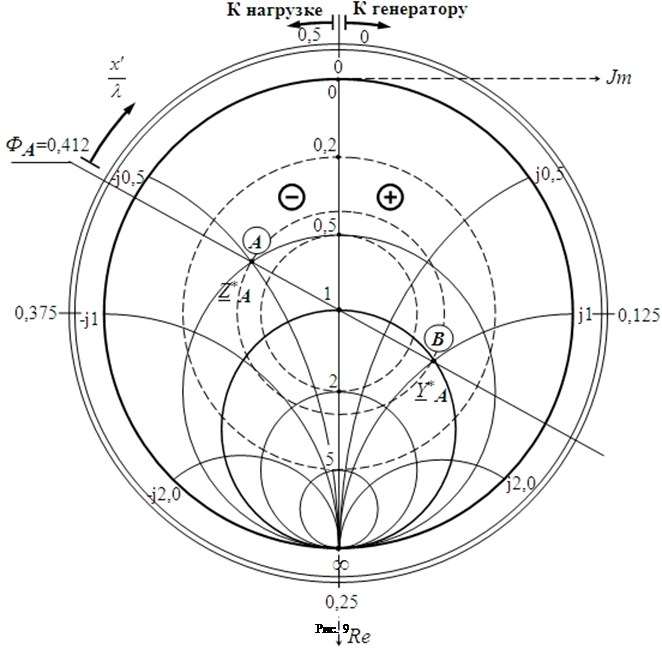
Диаграмма А. Р. Вольперта (ДВ, рис. 9) – номограмма относительных сопротивлений линии – это совокупность трех семейств окружностей постоянных К_бв, R^*, X^*, связанных общей зависимостью от координаты х¢. Для удобства вещественную ось располагают вертикально. Отметим ряд свойств ДВ.

1. Вертикальный диаметр (вещественная ось) является геометрическим местом (ГМ) чисто активных сопротивлений (X ^*=0) от R^*=0 в верхней точке до R^*=∞ в нижней. Слева от вертикального диаметра реактивности отрицательные, справа – положительные. Отрезок диаметра от 0 до 1 – ГМ узлов напряжения, от 1 до ∞ – ГМ пучностей напряжения. Центр диаграммы соответствует полному согласованию (n₂ = 0 и К_бв= 1).

2. Внешняя окружность ДB означает:

- ГМ чисто реактивных сопротивлений (R^*=0),

- коэффициент отражения n₂=1 (полное рассогласование),

- К_бв=0.

3. Любая точка в пределах ДBможет рассматриваться как место пересечения линий R^* и X* , т.е. как комплекс нормированного сопротивления линии Z^*=R^*+jX^*  в произвольном сечении х¢. Например, в точке А с условной фазой Ф_А=0,412  .

4. На ДB численные значения К_бв (пунктирные концентрические окружности) совмещают с соответствующими значениями   R^*= 0 ÷ 1   на вертикальном диаметре, поскольку в узлах напряжения они совпадают .

 

5. Диаграмму Вольперта - номограмму относительных сопротивлений линии можно рассматривать и как номограмму относительных проводимостей с теми же обозначениями и численными значениями.

Рассмотрим на ДB (рис. 9) точку В, диаметрально противоположную точке А (), что соответствует перемещению по физической линии на расстояние .

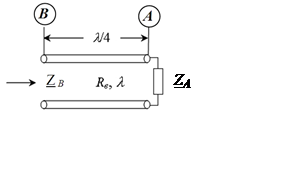
Напомним, что четвертьволновый отрезок  линии  (рис. 10)  трансфор-

мирует относительное  сопротивле-

ние в относительную проводимость.

По соотношению

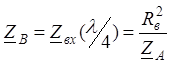 получим

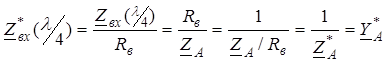.               Рис. 10

Таким образом, если в точке А задать сопротивление , то в диаметрально противоположной точке В   . Если же в точке В задать сопротивление , то в точке А   , т. е. ДB можно рассматривать как номограмму относительных проводимостей c той же разметкой и числами.

6. Для привязки конкретного входного сопротивления линии к конкретной её координате служит шкала условных фаз в долях длины волны  в пределах от 0 до 0,5.

Условная фаза произвольного сечения  а-а  линии с координатой x¢ определяется аргументом вектора  и складывается из аргумента j _n2 коэффициента отражения от нагрузки и условной фазы отрезка линии

Конец вектора  означает . Место на шкале условных фаз как точка пересечения с лучом, проведённым из центра ДB через , означает аргумент  КО и является условной фазой нагрузки   Ф_н = j _n2 .

Отсчёт координаты х¢, т. е. в направлении от нагрузки к генератору, производят от условной фазы нагрузки  по ходу часовой стрелки (рис. 9). В противном случае при перемещении от генератора к нагрузке отсчёт координаты x производят от фазы входного сопротивления линии  против часовой стрелки.

Вывод

Движению по физической линии от нагрузки к генератору на ДB соответствует перемещение по окружности постоянного К_бв по ходу часовой стрелки и наоборот.

2. Применение диаграммы Вольперта

2.1. Измерение комплекса сопротивления нагрузки с помощью измерительной линии

Измерительной линией называют участок рабочей линии, снабжённый индикатором напряжения (прибором) и метрической шкалой (рис. 11), по которой фиксируют положение индикатора.

 

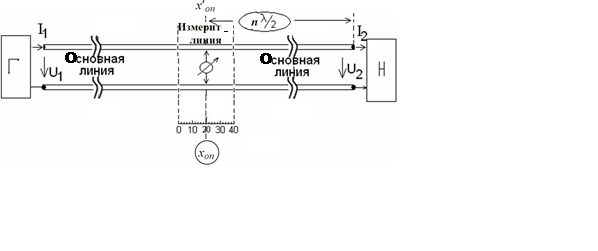Рис. 11

Измерительный прибор как индикатор напряжения на высоких частотах должен удовлетворять следующим требованиям. Сам прибор не должен нарушать однородность линии, его входное сопротивление должно быть большим и реагировать он должен только на напряжение, т. е. на электрическую составляющую электромагнитного поля. Одним из вариантов устройства для индикации напряжения является использование четвертьволнового отрезка такой же линии с прибором постоянного тока и диодом на конце. Поскольку вольт-амперная характеристика диода близка к квадратичной (), то отклонение стрелки прибора () пропорционально квадрату напряжения. Поэтому измеряемое напряжение пропорционально квадратному корню из показания прибора, т. е.   .

Измерение комплекса сопротивления нагрузки  с помощью измерительной линии основано на двух свойствах.

1-е свойство

Входное сопротивление линии в сечении, отстоящем от конца линии (нагрузки) на целое число полуволн, равно сопротивлению нагрузки

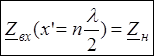
Это объясняется тем, что в синусоидальном режиме напряжение и ток вдоль линии периодически повторяются. Следовательно, через каждые полволны от нагрузки повторяется и входное сопротивление линии

.

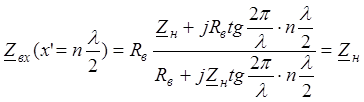Одно из сечений линии, отстоящее от нагрузки на целое число полуволн, называют опорной точкой. Следовательно,  .

2-е свойство

Входное сопротивление линии в узлах напряжения х_min известно:

по характеру оно чисто активно, а по модулю равно .

В относительных единицах     .

Порядок измерения(рис. 12, а)

1. Режим короткого замыкания (рис. 12, б) с целью определения длины волны λ и координаты опорной точки    .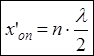

В режиме КЗ на конце линии наблюдается узел напряжения (). Поэтому все следующие к генератору узлы напряжения (x₁, x₂, x₃ …) отстоят от нагрузки на кратное число полуволн. Координату одного из них (x_оп) фиксируют на метрической шкале как опорную. Например x_оп = x₂.

Длину волны получают как удвоенное расстояние между двумя соседними узлами                  .

 

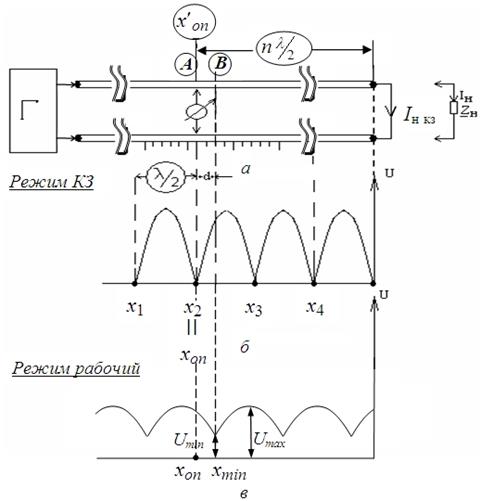
Рис. 12

2. Нагрузочный (рабочий) режим (рис. 12, в) с целью измерения 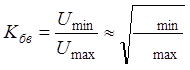 и определения координаты ближайшего к опорной точке узла напряжения   x_min.