![]()

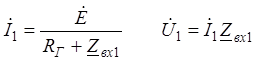
Выразим уравнения (6) и (8) через x = l – x¢.
![]()
|
|
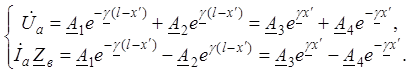
При x¢ = 0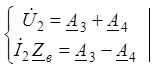
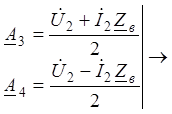 (6a) и (8a).
(6a) и (8a).
![]()
|

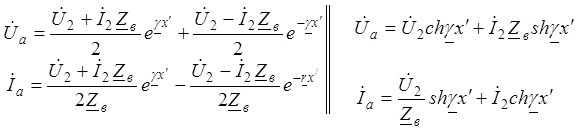
- расчетные соотношения для режима в произвольном сечении через известный режим на выходе.
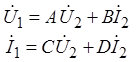
![]() Заметим, что всю линию (x¢=l) можно рассматривать как
четырехполюсник с матрицей [A]
Заметим, что всю линию (x¢=l) можно рассматривать как
четырехполюсник с матрицей [A]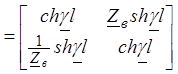 .
.
4. Входное сопротивление
линии в произвольном сечении x¢ получим из (14) делением почленно на ![]()
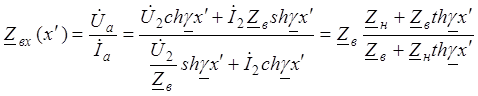 .
.
 Входное сопротивление в начале линии (x¢=l) зависит от Z в, Z н, l и
Входное сопротивление в начале линии (x¢=l) зависит от Z в, Z н, l и ![]()
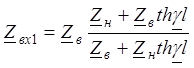 (15)
(15)
Заметим, что при условии ![]() (согласованная нагрузка)
(согласованная нагрузка)
![]()
![]() (15а)
(15а)
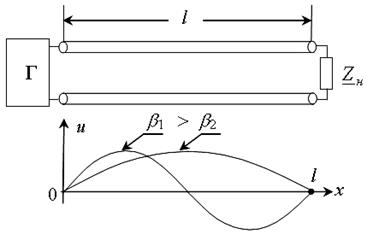
5. Волновые процессы в линии (длина волны, фазовая скорость, коэффициенты ослабления и фазы) рассмотрим на примере падающей волны напряжения.
Комплекс действующего значения напряжения
.(16)
Мгновенное значение напряжения
![]() .
.
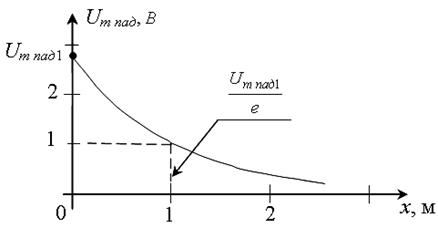
![]() Коэффициент ослабления (затухания) a = Re {
Коэффициент ослабления (затухания) a = Re {![]() }, Нп/м], характеризует уменьшение
амплитуды падающей волны на отрезке линии в 1 метр в направлении
распространения
}, Нп/м], характеризует уменьшение
амплитуды падающей волны на отрезке линии в 1 метр в направлении
распространения ![]() .
.
|
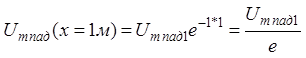 Если, например,
Если, например, Рис. 2
 Фазовая скорость uф,м/с, - скорость
перемещения по линии электромагнитного процесса с фиксированной
фазой Ф = wt - bx + yпад 1= const.
Фазовая скорость uф,м/с, - скорость
перемещения по линии электромагнитного процесса с фиксированной
фазой Ф = wt - bx + yпад 1= const.
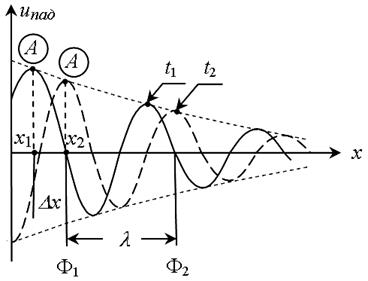
На рис. 3 представлены графики распределения мгновенного напряжения вдоль линии ( “ фотогра -
|
Поскольку фазу падаю-
щей волны считаем неизменной (т. А), то производная ее по времени равна нулю.
Рис. 3
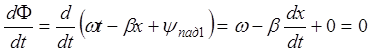 ®
® 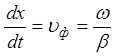 ®
®

![]()
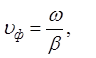 - фазовая скорость. (17)
- фазовая скорость. (17)
Если сделать несколько “фотографий” и просмотреть их как кадры в кино, то получим картину непрерывного перемещения процесса с фазовой скоростью. Для воздушной линии с малыми потерями uф = с =3×108 м/с.
Длина волны l, м, – расстояние между двумя ближайшими точками линии, фазы колебания в которых отличаются на 2p радиан (рис. 3). Ф1 - Ф2 = (wt1 - bx + yпад 1) - [wt1 - b(x + l)+ yпад 1] = 2p ®
 bl = 2p ®
bl = 2p ® 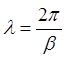 , м
, м
Отметим, что для воздушной линии на частоте f= 50 Гц длина волны l = 6000 км, на частоте f= 50 МГц - l = 6 м (с учетом того, что uф = lf).
 Фазовый коэффициент
Фазовый коэффициент

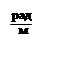
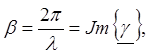 характеризует
скорость изменения фазы колебаний по координате x(рис. 4).
характеризует
скорость изменения фазы колебаний по координате x(рис. 4).
![]() Согласно
(16)
Согласно
(16)
фаза колебания при переме-щении волны от генератора к нагрузке линейно уменьшается Рис. 4
(jа = -bx),
т. е. в более удаленную от генератора точку волна приходит с запозданием по
времени на 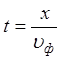 , с, и соответственно по фазе на
, с, и соответственно по фазе на
jа = -bx
= -2p![]() ,
рад.
,
рад.
Фазовый коэффициент b означает разность фаз колебаний напряжения на концах отрезка линии длиной в 1 метр j(x=1 м) = -bx= = -b, рад. Если b = 1 рад/м, то на концах отрезка линии в 1 метр разность фаз колебаний равна 1 радиан.
В технике используется понятие электрической длины
линии jL = bl = 2p![]() , рад. Линию считают “длинной”, если
на ней укладываются несколько волн или заметная часть волны. Ту же самую
физическую линию считают “короткой”, если на ней укладывается незначительная
часть волны. Критерием может стать отношение
, рад. Линию считают “длинной”, если
на ней укладываются несколько волн или заметная часть волны. Ту же самую
физическую линию считают “короткой”, если на ней укладывается незначительная
часть волны. Критерием может стать отношение ![]() =10-3, при
котором разность фаз колебаний на концах линии равна jL = 2p
=10-3, при
котором разность фаз колебаний на концах линии равна jL = 2p![]() = 2π×10 -3рад º 0,36°, т. е. практически незаметна.
= 2π×10 -3рад º 0,36°, т. е. практически незаметна.
![]()
![]() Постоянная
распространения линии
Постоянная
распространения линии
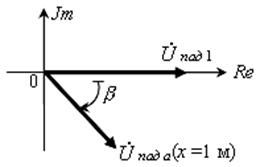
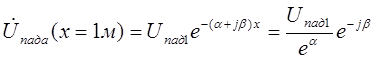 характеризует
изменение и амплитуды и фазы напряжения падающей волны вдоль линии. На отрезке
линии в 1 метр амплитуда уменьшается в еa
раз, а фаза отстает на β радиан (рис. 5)
характеризует
изменение и амплитуды и фазы напряжения падающей волны вдоль линии. На отрезке
линии в 1 метр амплитуда уменьшается в еa
раз, а фаза отстает на β радиан (рис. 5)
|
|
3. Условия неискажающей передачи
Сигналы, передаваемые по линии, занимают определенный частотный спектр. Передача сигнала будет неискажающей, если колебания всех частот спектра будут затухать одинаково [α (w) = const] и перемещаться по линии с одинаковой фазовой скоростью [uф (w) = const].
Если α (w) ≠ const, то колебания разных частот спектра сигнала затухают по-разному и спектр сигнала на выходе искажается. Такие искажения называют амплитудными.
Если uф(w) ≠ const, то колебания разных частот спектра сигнала перемещаются по линии с разными скоростями. В результате к концу линии сигнал “расползается” и искажается по форме. Такие искажения называют фазовыми.

|
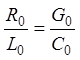
Хевисайда
С учетом (18) постоянная распространения

![]()
|
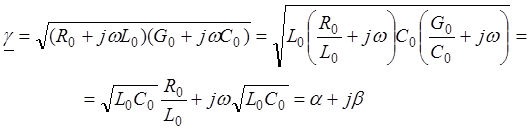
![]()
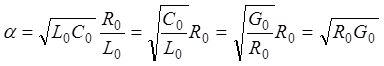 ® (19)
® (19)
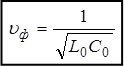 Фазовая
скорость
Фазовая
скорость 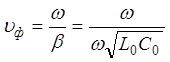 ® (20)
® (20)
Таким образом, в линии без искажений коэффициент затухания α (19) и фазовая скорость uф (20) не зависят от частоты.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.