Нагнетатели. Краткий обзор истории развития нагнетателей. Основные типы и классификация нагнетателей. Рабочие параметры нагнетателей, страница 5

l_н = h₂ – h₁ + ()/2+ q_o.c. + q (z₂ –  z₁).                                                                (4.16)

Для компрессоров последний член правой части опускают.

Выражая (4.16) через энтальпии, получим:

l_н = h₂ – h₁ + q_o.c..              (4.17)

С достаточной точностью процессы в нагнетателях можно считать адиабатным (q_o.c. = 0). Тогда:

                                                           .                  (4.18)

Для определения работы нагнетателя можно использовать диаграммы состояния.

При равенстве скоростей на входе и выходе из нагнетателя можно записать:

                                                        l_н = с_р (Т₂ – Т₁).               (4.19)

Выражение (4.19) удобно для оценки работы и КПД нагнетателя по данным испытаний.

Изменение энергии газа выражается I законом термодинамики:

                                                         dq = dh – ν∙dp,                (4.20)

где ν∙dp учитывает работу на повышение давления и перемещения газа и называется полной работой повышения давления.

Интегрируя (4.20), получим работу сжатия в форме:

l_с = h₂ – h₁+q _o.c.+q_тр,           (4.21)

где q_тр – теплота трения.

При q _o.c. = 0 имеем:

l_с = h₂ – h₁ + q_тр.               (4.22)

Таким образом, работа сжатия l_с совпадает с технической работой.

Решая совместно (4.16) и (4.21), получаем выражение закона сохранения энергии в механической форме – уравнение Бернулли (q_тр = l_тр):

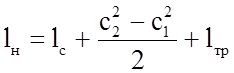                                                    ,           (4.23)

т. е. работа, подведенная к нагнетателю, расходуется на повышение давления потока, повышение его кинетической энергии и преодоление потерь.

Другая форма уравнения Бернулли:

                                      .                                                                (4.24)

Решая (4.24) относительно l_н, получим выражение (4.23).

4.6. Процессы сжатия в диаграммах состояния

Для оценки совершенства процессов в нагнетателях, установления потерь и определения КПД используется сопоставление идеального и реального процессов сжатия.

При рассмотрении процессов чаще всего используются диаграммы состояния h-s и T-s, а также эксергетическая диаграмма е – h.

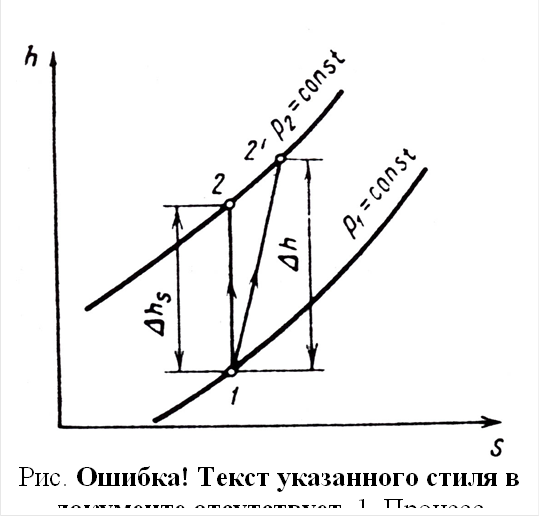На рис. 4.11 представлен идеальный процесс 1 – 2 сжатия газа в компрессоре на h-s диаграмме при отсутствии теплообмена с окружающей средой.

Отрезок на диаграмме ∆h_s – работа процесса сжатия, т. е. разность энтальпий в конце и начале процесса.

При наличии потерь конечное состояние газа определяется мягкий 2' (при S₂ > S₁). Если и здесь теплообмен отсутствует, то работа процесса равна разности энтальпий h_2' – h₂ (отрезок ∆h_s).

Взаимосвязь параметров уравнения (4.21) удобнее анализировать с помощью T-s диаграммы (на рис. 4.12; рис. 4.13).

В этом случае работа сжатия и разность энтальпий изоэнтропийного процесса можно определить площадью F₁₂₃₄₅.

Рис. 4.12. Процесс сжатия в диаграмме Т-s (q o.c. = 0)	Рис.4.13. Процесс сжатия в диаграмме Т-s (q o.c. ≠ 0)

В действительном процессе (q_тр ≠ 0, q _o.c. = 0) разность энтальпий и работа определяется площадью F_342'>F_12345'.

При сжатии рабочего тела в компрессоре выделяется значительное количество теплоты, тем больше, чем выше степень повышения давления р₂/р₁.

В результате увеличивается затрата работы на сжатие и возникает возможность перегрева, концентрации напряжений в деталях. Поэтому применяют охлаждение газа в процессе сжатия.

Пусть процесс сжатия при теплообмене с окружающей средой изображены в диаграмме Т – S (рис. 4.13).

При интенсивном теплообмене процесс сжатия отклоняется влево (конечное состояние газа определяется точкой 2').

Разность энтальпий тогда определяется площадью F_2'452'', а количество отведенной теплоты – площадью F_2'134.

Из сопоставления работы адиабатного и изотермического сжатия следует также, что разница работ растет с увеличением отношения давлений. При
р₂/р₁ = 2 эта разница составляет 9,5 %, а если р₂/р₁ = 4, то она достигает 18,6 %.