Нагнетатели. Краткий обзор истории развития нагнетателей. Основные типы и классификация нагнетателей. Рабочие параметры нагнетателей, страница 4

Мощность, подводимую на вал нагнетателя от приводного двигателя, называют мощностью нагнетателя и обозначают N, кВт.

Энергетическое совершенство насосов и вентиляторов оценивается КПД:

                                                           .                     (4.9)

Значение КПД всей установки будет:

                                                        .                (4.10)

где N_эл – электрическая мощность, подводимая к двигателю.

4.4. Совместная работа нагнетателя и трубопроводной системы. Характеристика и рабочая точка системы

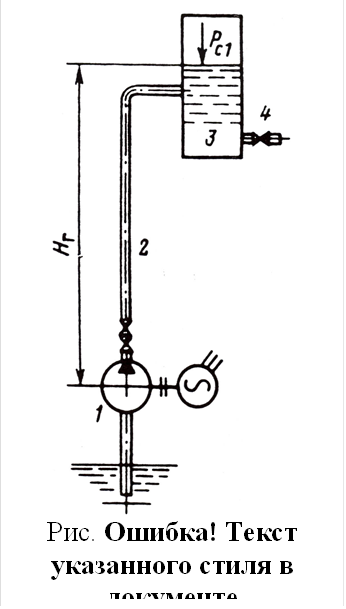Рассмотрим систему, состоящую из нагнетателя 1, трубопроводной сети
2 и емкости 3, в которой задвижкой 4 поддерживается постоянное статическое давление (рис. 4.9). В этом случае нагнетатель преодолевает статическое давление и сопротивление системы трубопроводов, вызванное вязкостью перемещаемой среды.

Предположим, что работа системы ста­ционарна, т.е. неизменна, независима от времени. Основное условие стационар­ности: энергия, сообщаемая нагнетате­лем потоку рабочего тела, равна энергии, затрачиваемой потоком на преодоление статического давления и сопротивления системы. Если это положение не соблю­дается, то очевидно, происходит или раз­гон потока, или замедление его, т. е. име­ет место нестационарность.

Если массовая подача нагнетателя m_н, кг/с; массовый расход через трубопроводную систему m_тр, кг/с, то при отсутствии уте­чек (абсолютно плотная система)

                                                              m_н = m_тр                             (4.11)

или

                                                         ρ_н V_н= ρ_тр V_тр,                 (4.12)

где V_н и V_тр – объемные производительности (подачи) нагне­тателя.

Выходное сечение нагнетателя и входное сечение трубопро­вода совпадают, и поэтому ρ_н = ρ_тр. Следовательно,

                                                             V_н = V_тр.                     (4.13)

По значению V_тр рассчитывается значение средней скорости с, в выходном сечении нагнетателя, необходимое для расчета сопротивления системы.

Допуская, что система работает в условиях стационарности, имея ввиду, что p = ρ∙g∙H, можно записать с учетом уравнения сохранения удельной энергии потока и после преобразований:

                                                        ,               (4.14)

где а – коэффициент пропорциональности (качество системы); H_н, H_ст – напоры нагнетателя стационарный.

Левая часть уравнения (4.14) зависит от подачи нагнетателя и является напором. Правая – напор, необходимый в системе для поддержания статистического давления и компенсации потерь напора в ней.

Изобразим правую часть уравнения (4.14) графически в системе V-H.

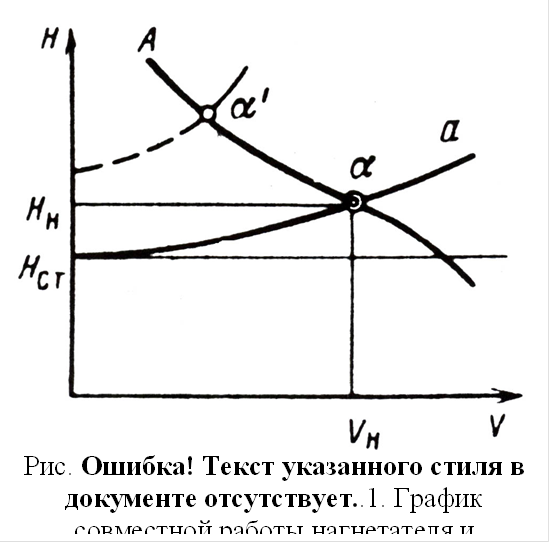Получим квадратическую параболу называемую характеристикой трубопроводной системы.

Нагнетатель любого данного типа размера обладает определенной формой напорной характеристики V-H.

Построив такую характеристику А, получим точку α пересечения характеристик, называемую рабочей точкой системы.

Точка α определяет режим работы системы и, следовательно, рабочие параметры V-H.

Если вводить в систему дополнительные сопротивления и повышать статистическое давление в емкости 3 уменьшая пропуск рабочей среды через запорное устройство 4, то характеристика сети расположится выше и будет более крутой (штриховая линия), рабочая точка займет новое положение α', подача нагнетателя уменьшится, напор возрастет.

Такой графический метод для выбора нагнетателя и анализа работы системы используется в практике проектирования.

4.5. Закон сохранения энергии в механической форме – уравнение         Бернулли

Количественное описание процессов в нагнетателях базируется на основных законах термодинамики и их следствиях.

Для элементарного процесса в системе нагнетатель – окружающая среда уравнение энергетического баланса имеет вид:

                                            dl – dq_o.c. = dh+ d(с²/2)+ d(gz).   (4.15)

Интегрируя уравнение (4.15) в пределах, соответствующих сечениям входа и выхода, получим выражение для работы: