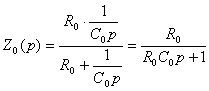Расчет системы автоматической стабилизации для требуемой точности и устойчивости процессов, страница 9

        ;(5.2) 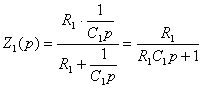                 ;    (5.3)

Подставляя формулы (5.2) и (5.3) в (5.1), окончательно можно записать передаточную функцию корректирующего блока :

                                       ;           (5.4)

где	kРБ = Ro / R1=1,95
	Т1КУ = R1C1
	ТоКУ = RoCo

Пусть R_o = 10⁶ Ом. 

Тогда  R₁ = R_o / k_РБ = 512820,5 Ом.

Структурная схема скорректированной системы представлена на (рис. 5.2).

 В соответствии с теорией устойчивости, можно принять :

T₁^КУ = T₁ = 0,42 c,   (=0,64)

T_o^КУ = 0,1·T₃ = 0,01 c

Тогда Cо = T_o^КУ / R_о = 0,01 / 10⁶ =  0,01 мкФ, 

           C₁ = 2 мкФ    ( =1,25 мкФ)

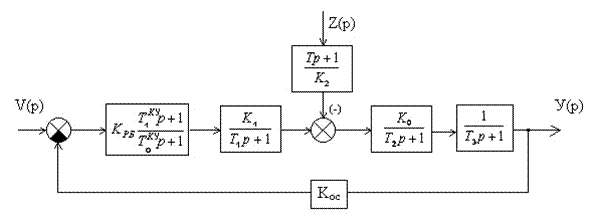
Рисунок 5.2  Структурная схема скорректированной системы (вариант 1).

где	T1 = 0,42 c   ( =0,64 )
	T2 = 0,9 c
	T3 = 0,1 c

Для определения передаточной функции по управляющему воздействию, необходимо принять значение возмущающего воздействия Z=0. Тогда передаточная функция скорректированной системы по управляющему воздействию :

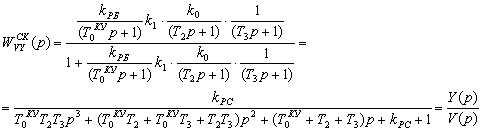                         (5.5)

Для определения передаточной функции по возмущающему воздействию, необходимо принять значение V=0. Тогда передаточная функция скорректированной системы по возмущающему воздействию :

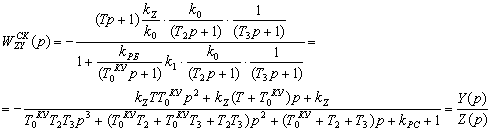                      (5.6)

Т.к. устойчивость не зависит от вида рассматриваемого входного сигнала, то положим Z = 0.

Тогда анализ устойчивости можно проводить по схеме, представленной на (рис 5.3).

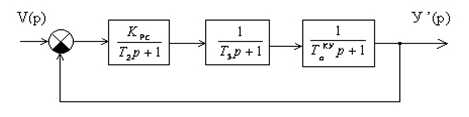
Рисунок 5.3  Структурная схема скорректированной системы (вариант 2).

где	kрс = kтрс = kРБ k0 k1 = 39

5.2  Анализ устойчивости скорректированной системы

5.2.1  Анализ системы по критерию Гурвица.

Найдем значение k^г_рс  для скорректированной системы, используя (4.8) :

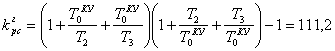                             ;   (так же)                              (5.8)

Поскольку  k_рс < k^г_рс   в 2,9 раза, то система устойчива.