Расчет системы автоматической стабилизации для требуемой точности и устойчивости процессов, страница 6

Суть критерия Гурвица: для того, чтобы система была устойчивой необходимо и достаточно, чтобы при a_n >0 все определители Гурвица (диагональные миноры) были положительными:

D₁ = a_n-1 > 0

D₂ = a_n-1a_n-2 - a_na_n-3 > 0                                                                       (4.4)

…

D_n = a₀ D_n-1 > 0

На основе (2.10) и (4.2) можно записать характеристическое уравнение системы 3-й степени в замкнутом состоянии:      ;            (4.5)

a3=0,64*0,9*0,1=  0,0576;

a2=0,64*0,9+0,64*0,1+0,9*0,1=  0,73

a1=0,64+0,9+0,1=  1,64

a0=Kрб*K1*K0*1  +1=1*50*0,4*1+1= 21

где	a3 =	T1T2T3 = 0,42 * 0,9 * 0,1 = 0,0378
	a2 =	T1T2 + T1T3 + T2T3 = 0,42*0,9 + 0,42*0,1 + 0,9*0,1 = 0,51
	a1 =	T1 + T2 + T3 = 0,42+0,9+0,1 = 1,42
	a0 =	kрс + 1 = 1*80*0,25*1 + 1 = 21

Из коэффициентов характеристического уравнения (4.5) составим главный определитель Гурвица 3-го порядка:

                   a₂    a₀     0

                D₃ =        a₃    a₁     0           (4.6)

                    0    a₂     a₀

Для того, чтобы линейная система была устойчивой, необходимо и достаточно, чтобы

при а₃ > 0, все определители Гурвица были положительными.

a₃ = 0,0378   (0,0576)  > 0

D₁ = a₂ =  0,51   (0,73)  > 0

D₃ = a₀ D₂,       где a₀ = 21

D₂= a₂a₁ – a₀a₃ = 0,51*1,42- 21*0,0378 =  - 0,07   (0,73*1,64-21*0,0576= - 0,0124)  < 0

Система является неустойчивой, т.к. определитель Гурвица 2-го порядка является отрицательным.

Приравняв главный определитель Гурвица к нулю, найдем условие граничного значения передаточного коэффициента в замкнутом состоянии:

D₃ = a₀ D₂ = 0. Т.к. a₀ = k_рс + 1 > 0,   то

D₂ = 0 = (T₁T₂ + T₁T₃ + T₂T₃)(T₁ + T₂ + T₃) – (k^г_рс + 1) T₁T₂T₃                                              (4.7)

         Из  (4.7) найдем k^г_рс :

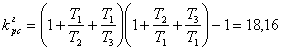    (=19,78)                                                           (4.8)

Т.к.  k_рс = k_РБ×k₀×k₁×k_oc = 20,  и  k_рс > k^г_рс, то система неустойчива.

4.2  Устойчивость системы по критерию Найквиста.

Для анализа устойчивости системы по критерию Найквиста приведем структурную схему (рис 2.8) к одноконтурной схеме, учитывая k_ос = 1, и учитывая соотношения между постоянными времени T₂>T₁>T_3.