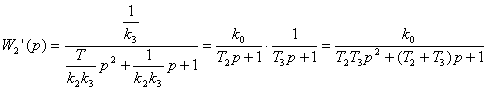Расчет системы автоматической стабилизации для требуемой точности и устойчивости процессов, страница 4

        ;                       (2.7)

            На основе (2.7) можно записать следующую систему уравнений:

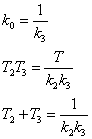                (2.8)    Решая систему уравнений (2.8) получаем корни: Т₂ = 0,86 и Т₃ = 0,14                                   (T2=0,89, T3=0,11)      Окончательно, получаем результат:

                              ;   (2.9)         где    T₂ = 0,9

                                                                                                      T₃ = 0,1

                                                                                                      k₀ = 0,25 ;  (=0,4)

Пусть W₂’(p) = W₂(p)× W₃(p). Тогда упрощенная структурная схема выглядит следующим образом см. (рис 2.8).

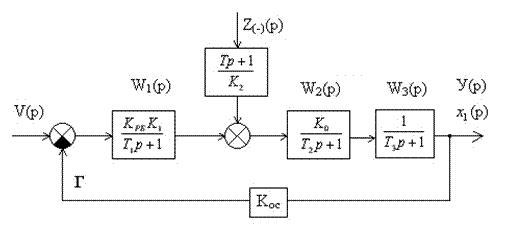
Рисунок 2.8 – Преобразованная структурная схема (вариант 3).

            Для определения передаточной функции системы по управляющему (задающему) воздействию W_VY(p) необходимо принять Z = 0 :

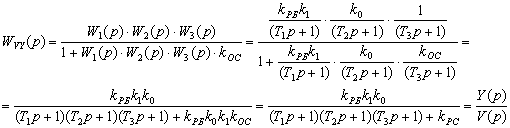                         (2.10)

        где  k_рс = k_РБ×k₀×k₁×k_oc – передаточный коэффициент разомкнутой системы.

Изображение выходного сигнала в операторном виде :   Y(p) = W_VY(p)×V(p) ;          (2.11)

Для определения передаточной функции системы по возмущающему воздействию W_ZY(p) необходимо принять V = 0. Тогда можно записать:

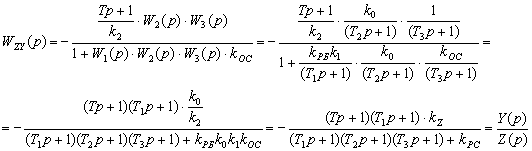                                (2.12) 

       где  k_z = k₀/k₂ – передаточный коэффициент по возмущающему воздействию;

              k_рс = k_РБ×k₀×k₁×k_oc – передаточный коэффициент разомкнутой системы.

    Изображение выходного сигнала в операторном виде :

                                        Y(p) = W_ZY(p)×Z(p)  ;                    (2.13)

Используя принцип суперпозиции, на основе (2.11) и (2.13) можно записать изображение выходного сигнала всей системы :

                                         Y(p) = W_VY(p)×V(p) + W_ZY(p)×Z(p)  ;                  (2.14)

Подставив в (2.14) результат из формул (2.10) и (2.12),  окончательно можно записать изображение выходного сигнала всей системы:

      ;              (2.15)

3  СТАТИЧЕСКИЙ  РАСЧЕТ системы

            Пусть k_ос = 0, т.е. рассматривается разомкнутая система (без обратной связи).

Тогда на основе формулы (2.15) с учетом теоремы операционного исчисления "о предельных значениях" при  p = 0 можно записать уравнение статики вида :

                              y = k_РБ×k₁×k₀×V – k_z×Z =  y^п - Dy_{рс     ;}                         (3.1)

где	yп –	полезная составляющая выходного сигнала в разомкнутой системе;
	Dyрс –	величина, на которую уменьшается выходной сигнал в разомкнутой системе из-за влияния возмущающего воздействия.