Расчет системы автоматической стабилизации для требуемой точности и устойчивости процессов, страница 5

               Dy⁰_рс =  k_z×Z₀ = k₀/k₂×Z₀ = 0,25/0,25 × 20 = 20   ( 0,4/0,4*20=20 ) > = 0,5  ;    (3.2)

где

Z0 –

максимальное значение возмущающего воздействия (на эту величину уменьшается выходной сигнал).

 Пусть y₀ =  k_РБ×k₁×k₀×V – значение выходной координаты системы до тех пор пока еще не начало действовать возмущающее воздействие. Тогда уменьшение значения выходной координаты можно показать на рис 2.9 :

                            Рисунок 2.9 – Статическая характеристика разомкнутой системы.

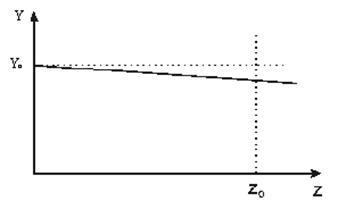Поскольку Dy⁰_рс >, то разомкнутая система не удовлетворяет с точки зрения стабилизации и должна быть заменена замкнутой системой автоматической стабилизации. Для замкнутой системы k_ос = 1.

 Подставляя p = 0  в  формулу (2.15), получим :     ;         (3.3)

Поскольку задание на проектирование предполагает, что для замкнутой системы ошибка регулирования не должна превышать , т.е. должно быть выполнено условие (3.4),

                                       ;                (3.4)

то будем подбирать k_рс таким, чтобы выполнялось условие (3.4).

Используя знак " = " в условии (3.4), окончательно можно записать расчетную формулу требуемого значения передаточного коэффициента разомкнутой системы:

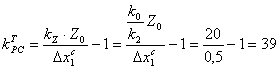                                    ;  (так же)                   (3.5)

                    где k^т_рс – требуемый коэффициент разомкнутой системы.

С учетом того, что k_рс = k_РБ×k₀×k₁×k_oc = k^т_рс, можно рассчитать требуемое значение k_РБ :

                      ;  (39/0,4*50*1 = 39/20 = 1,95)                (3.6)

При  k_РБ = 1,95 обеспечивается заданная точность стабилизации выходной координаты системы.

4  АНАЛИЗ УСТОЙЧИВОСТИ ИСХОДНОЙ СИСТЕМЫ

Устойчивость – это свойство системы возвращаться в прежнее состояние равновесия после вывода ее из этого состояния и прекращения действия возмущения.

Необходимым условием устойчивости линейной системы любого порядка является положительность коэффициентов ее характеристического уравнения.

Находить корни алгебраических уравнений высоких степеней затруднительно, а численные методы не дают общих формул.

Рассмотрим алгебраический критерий устойчивости Гурвица.

Устойчивость системы по критерию Гурвица

Поскольку у нас найдена передаточная функция системы в замкнутом состоянии:

 ;             (4.1)

то, приравнивая знаменатель к нулю, можно записать характеристическое уравнение системы в замкнутом состоянии:

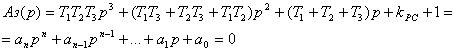                                    (4.2)

Из коэффициентов характеристического уравнения составляется главный определитель Гурвица:

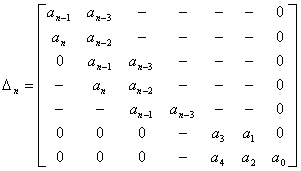                                                                  (4.3)