Передаточные функции системы автоматического управления. Типовые воздействия в автоматике переходная характеристика звена. Импульсное входное воздействие

Передаточные функции системы автоматического управления.

Типовые воздействия в автоматике

         переходная характеристика звена

 Импульсное входное воздействие.

Правило определения W – функции при подаче импульсного воздействия.

Стандартные звенья

Частотные характеристики звеньев САУ

Формулы Эйлера (формулы связи)

годограф вектора

Устойчивость систем автоматического регулирования

Методы определения устойчивости

Условие устойчивости

 Теорема ляпунова

Критерий устойчивости Раусса.

 Критерий Гурвица.

Частотные критерии устойчивости.

Критерий устойчивости по Михайлову.

Критерий устойчивости Найквиста.

Влияние параметров системы на ее устойчивость.

D-разбиение плоскости одного комплексного числа.

Передаточные функции системы автоматического управления.

Все рассмотренные типовые звенья могут быть объединены в виде различных соединений звеньев: последовательного, параллельного и встречно-параллельного. Правила определения передаточной функции системы (см. структурные преобразования МОТС).

? Привести схему замещения объединенных соединений двух элементарных звеньев: пропорционального и интегрирующего) Таблицу Лапласа…

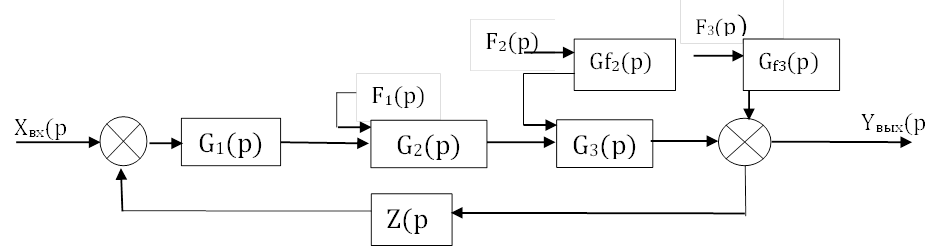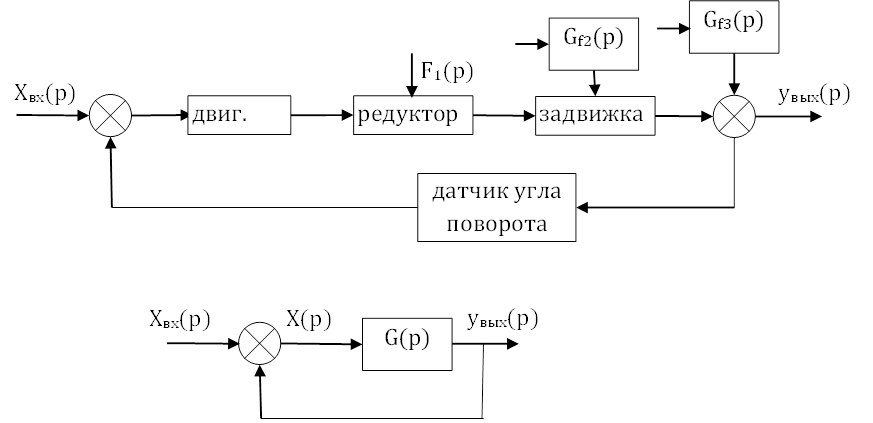
Рассмотрим структурную схему с возмущающими воздействиями:

Возмущающие воздействия F₂ и F₃ действуют на входе звеньев в прямой цепи через дополнительные звенья G_f2 и G_f3, которые отражают характер зависимости системы от конкретного возмущающего воздействия.

Определим зависимость системы от возмущающих воздействий. В силу линейности рассматриваемых систем к ним применим принцип наложения, который позволяет определить общую реакцию системы, то есть изменение выходной величины как сумму частных реакций от каждого из внешних воздействий в отдельности.

Пусть  запишем сигналы, действующие на звено G₂:

Запишем выражение для выходного сигнала:

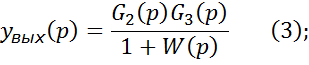
Операторное выражение выходной величины системы равно дроби, числитель которой есть произведение изображения внешнего воздействия на передаточные функции звеньев, выключенных последовательно между точкой приложения внешнего воздействия и выхода систем, а знаменатель это увеличенная на 1 передаточная функция разомкнутой системы.

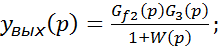
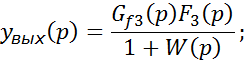
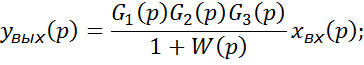
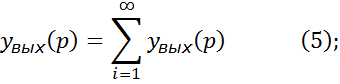
Из выражения (5) можно получить выражение передаточной функции по величине и по ошибке. Особенностью является передача выходного сигнала к элементу сравнения, то есть на вход системы с коэффициентом передачи равным 1.

Основным видом внешних воздействий в следящей системе считается входное управляющее воздействие, которое система отрабатывает с некоторой ошибкой рассмотрения.

учтем что обратная связь равна 1:

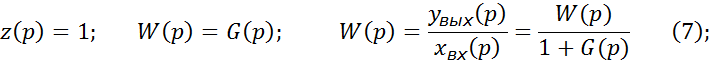
Выразим из (6) величины выходного сигнала:

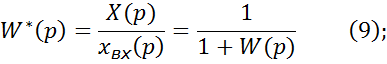
Выражение передаточной функции по ошибке.

Типовые воздействия в автоматике.

Характер переходных процессов зависит от состава системы и от формы входного сигнала. Входные сигналы могут иметь различную форму. При исследовании новых устройств автоматики применяют сигналы определенной формы, которые называют типовыми воздействиями:

1)  скачок входного сигнала или единичное ступенчатое воздействие;

2)  скачок скорости входного сигнала или импульсная функция;

3)  гармоническое входное воздействие или синусоидальный входной сигнал.

1. Пусть на вход звена подается ступенчатое воздействие, тогда выходная величина этого звена определяется видом его дифференциального уравнения.

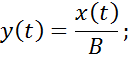
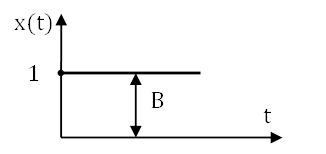
Отношение выходной величины звена при входном воздействии в виде ступенчатой функции к координате этой функции при нулевых начальных условиях и отсутствии возмущающих воздействий называется переходной характеристикой звена:

Обычно в качестве переходной функции рассматривают не отношение выходной величины y(t) к ординате В, а непосредственно выходную величину y(t) при условии, что входное ступенчатое воздействие является единичным.

Зная переходную функцию звена всегда можно определить его передаточную функцию:

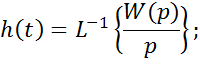
Правило определения передаточной функции при ступенчатом воздействии:

1.  подаем на вход единичную функцию;

2.  определяем переходную функцию вида h(t);

3.  определяем по таблице изображений h(p);

4.  по формуле связи переходной и передаточной функции определяем передаточную функцию

Импульсное входное воздействие.

Пусть на вход звена подается импульсное воздействие х(t)=Cδ(t)      (1),

δ (t) – функция удовлетворяющие условиям:

при t ≠ 0  δ(t) = 0;

t = 0  δ(t) = ∞.

При этом на выходе звена будет сигнал g(t) =       (2).

g(t) представляет собой отношение выходной величины звена, при входном воздействии в виде  импульса, к площади этого импульса при нулевых начальных условиях и отсутствии начальных возмущающих воздействий, такой сигнал называется функцией веса.

Обычно в качестве функции веса рассматривается непосредственно выходная величина при условии, что входная импульсная функция является единичной, то есть площадь импульса С = 1.

g(t) = W(p)δ(t);

L[g(t)] = W(p)∙L[δ(t)];

g(p) = W(p)1 = W(p);