Передаточные функции системы автоматического управления. Типовые воздействия в автоматике переходная характеристика звена. Импульсное входное воздействие, страница 11

Для того чтобы определить является ли область (I) областью устойчивости выбирают из этой области какое-либо значение τ_1,2,3...  и проверяют устойчивость по любому критерию устойчивости. Так как число корней слева от мнимой оси одно и то же для всех τ лежащих внутри области (I), то если система является устойчивой для τ₁ то она будет устойчива для всех τ лежащих в этой области.

D-разбиение плоскости 2х параметров.

Рассмотрим влияние на устойчивость системы двух параметров, если эти параметры входят в линейное характеристическое уравнение kP(p)+τQ(p)+R(p)=0 (4). Q, R, P – это полиномы, коэффициенты которых не зависят от τ и k. Выделим области устойчивости плоскости τ и k, построив для этого кривую D-разбиения:

p → jω, kP(jω)+τQ(jω)+R(jω)=0 (5);

Выделим в полиномах действительную и мнимую часть: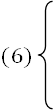

P(jω) = P₁(jω) + jP₂(ω);

Q(jω) = Q₁(jω) + jQ₂(ω);

R(jω) = R₁(jω) + jR₂(ω);

Подставляя (6) в (5) и группируя вещественные и мнимые части получим:

kP₁(jω) + τQ₁(jω) + R₁(jω) + j[kP₂(ω) + τQ₂(ω) + R₂(ω)] = 0 (7)

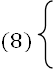Комплексная величина равна нулю, тогда и только тогда, когда одновременно вещественная и мнимая части равны нулю, поэтому запишем вместо выражения (7) систему из 2 уравнений:

kP₁(jω) + τQ₁(jω) = -R₁(jω)

kP₂(ω) + τQ₂(ω) = -R₂(ω)

Эта система позволяет определить k_x и τ_x при частоте ω=ω_x. Значения k_x и τ_x на плоскости τ и k определяют точку, которая принадлежит кривой D-разбиения. Чтобы найти все точки этой кривой следует решить методом определителей систему уравнений (8) относительно k и τ.

   

              

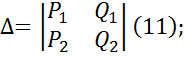
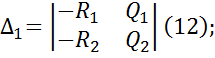
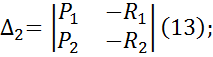
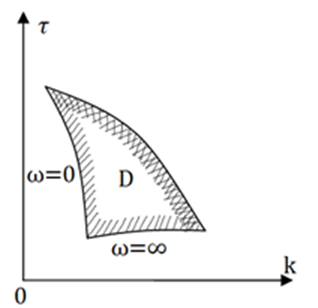
При Δ не равном 0 для каждого значения частоты уравнение (9) и (10) можно определить τ и k и, следовательно, построит в плоскости τ и k границу D-разбиения. k – по оси абсцисс, τ – по оси ординат. Если поменять местами столбцы определителя, то необходимо изменить обозначения осей на плоскости  τ ,k. Уравнения (9) и (10) справедливы только для тех частот, при которых уравнения системы (8) линейно-независимы и совместимы. При ω=0 и ω=∞ уравнения системы (8) перестают быть линейно-независимыми, так как Δ является непрерывной функцией частоты, и её знак может меняться при равенстве 0 и ∞. В этом случае, числитель и знаменатель (9),(10) могут оказаться равными 0 или ∞, поэтому граница D-разбиений по 2-м вещественным параметрам, которые строятся по уравнениям (9) и (10), при изменении частоты от -∞ до +∞, выполняется особыми прямыми, уравнения которых получаются подстановкой в (7) ω=0 и ω=∞.

Если указанные коэффициенты характеристического уравнения зависят от τ и k, то особая прямая стремится к ∞ и не вычерчивается. Кривая D-разбиения плоскости 2х параметров не симметрична относительно вещественной оси, но имеет совпадающие точки, соответствующие значения +ω и -ω, так как согласно выражениям (9) и (10) τ и k являются четными функциями частоты. А согласно (11) – основной определитель – нечетная функция. Если главный определитель равен 0, то это означает что кривой D-разбиения не существует, и все разбиения плоскости осуществляются особыми кривыми.  После построения кривой D-разбиения намечается предполагаемая область устойчивости:

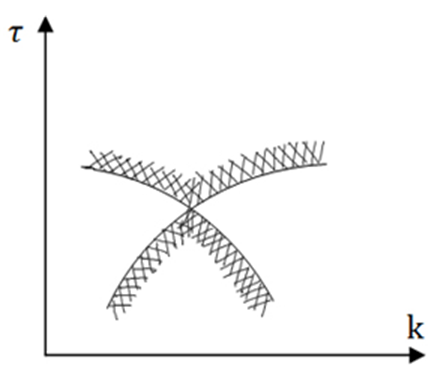
Если k откладывается по оси абсцисс, а τ по ординате, то двигаясь по кривой D-разбиения от -∞ до +∞ (частота), штрихуем левую сторону D-кривой при определителе Δ больше 0, и правую при Δ<0. При движении вдоль кривой знак определителя меняется только при пересечении с особыми прямыми, то есть при ω=0 и ω=∞. Так как кривая D-разбиений при изменении частоты от -∞ до +∞

проходится дважды, то ее и штрихуют дважды, оба раза с одной стороны, так как знак определителя при изменении знака частоты меняется на обратный. Штриховка особых прямых (одновременно заштрихованные и незаштрихованные стороны) D-кривой и особой прямой должны располагаться навстречу друг другу.

Получив плоскости τ и k области с одинаковым числом корней слева от мнимой оси определяют область  с наибольшим числом корней слева от мнимой оси. Выбирают в этой области какую-либо точку и проверяют на устойчивость исходное уравнение, в которое вместо τ и k подставляют координаты этой точки, и выясняют – устойчива это область или нет.