Передаточные функции системы автоматического управления. Типовые воздействия в автоматике переходная характеристика звена. Импульсное входное воздействие, страница 7

                                   

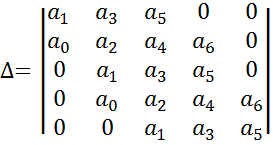
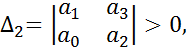
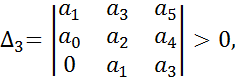
Номер диагонального минора определяет номер коэффициента по диагонали, для которого составлен данный минор. Последний столбец главного определителя содержит только один коэффициент а_n.

Критерий Гурвица формулируется следующим образом: чтобы характеристическое уравнение имело все корни с отрицательной вещественной частью, главный определитель и все его диагональные миноры должны иметь один знак с коэффициентом a₀ и быть больше 0. Для положительных коэффициентов уравнения a_n > 0, следовательно, главный определитель также > 0. Если определитель Δ_n-1 > 0 можно вычислять не все диагональные миноры главного определителя, так как некоторые из них приобретают положительные значения при положительности других миноров. Система находится на границе устойчивости, если выполняется условие Δ_n = a_n·Δ_n-1 = 0 (*). Это равенство возможно в двух случаях: a_n = 0 или Δ_n-1 = 0. В первом случае система находится на границе апериодической устойчивости, то есть один из корней характеристического уравнения равен 0. Во втором случае система находится на границе колебательной устойчивости, то есть два сопряженных корня находятся на мнимой оси. В большинстве случаев коэффициент a_n не равен 0. Если в этом случае система находится на границе устойчивости, то это граница колебательной устойчивости.

На основании выражения (*) при всех заданных параметрах системы, можно принять за неизвестных один параметр и определить его предельное значение, при котором система находится на границе устойчивости. Таким параметром обычно считают коэффициент усиления системы.

Критерий Гурвица рационально использовать при степени характеристического уравнения меньше или равно 4.

Частотные критерии устойчивости.

Эти критерии позволяют судить об устойчивости замкнутых систем по частотным критериям условно разомкнутых систем, без определения корней характеристического уравнения.

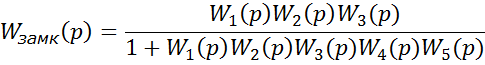
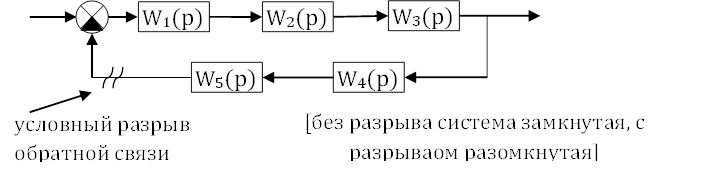
Частотные критерии являются графоаналитическими и позволяют определять устойчивость замкнутой системы при отсутствии характеристического уравнения и передаточных функций системы, используя экспериментально полученные частотные характеристики звеньев и разомкнутой системы в целом.

В основе частотных критериев устойчивости лежит, известный в теории функций комплексного переменного, принцип аргумента.

Пусть дано характеристической уравнения с замкнутой системой:

D(p) = a_npⁿ·a_n-1p^n-1+…+a₀ = 0 (1);

Разделим коэффициенты всех членов уравнения на коэффициент при старшем члене pⁿ и получим:

D(p)= (p- λ₁)(p- λ₂)…(p- λ_n) (2); где λ_i корни характеристического уравнения.

В этом разложении p=α+jω произвольное комплексное число, которое может быть представлено на комплексной плоскости в виде вектора, начинающегося в начале и оканчивающегося в точке, координаты которой соответствуют вещественной и мнимой частям комплексного числа.

Также любой i-тый корень может быть изображен на плоскости (на рисунке точка С).

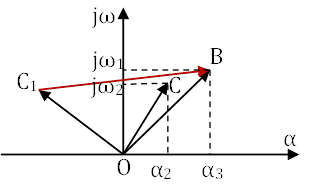Сомножитель p-λ_i может быть представлен вектором, начинающимся в точке C₁ и заканчивающимся в точке B. Произведем замену p на jω в выражении (2):

D(jω)=(jω- λ₁) (jω- λ₂)… (jω- λ_n) (3)

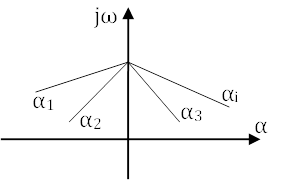
Тогда геометрическое представление комплексного числа на комплексной плоскости будет следующим – начало комплексного числа лежит в точке с координатой α_i, а конец на мнимой оси в точке с координатой jω.

Определим изменение положения вектора C₁B при изменении частоты от –∞ до +∞, то есть изменение аргумента D(jω).

 (4)

 (5) – изменение аргумента

при –∞ < ω < +∞ .

Согласно уравнению (5) для изменения аргумента необходимо подсчитать сумму в выражении jω-λ_i. Это изменения аргумента зависит от того, в какой – левой или правой полуплоскости лежит корень λ_i. Рассмотрим два случая:

Первый случай:

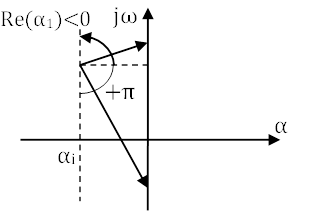λ₁ принадлежит левой полуплоскости, то есть вещественная часть отрицательна. При изменении частоты от –∞ до +∞ конец вектора jω-λ_i скользит вдоль мнимой оси снизу-вверх, поворачиваясь против часовой стрелки на 180̊.