Передаточные функции системы автоматического управления. Типовые воздействия в автоматике переходная характеристика звена. Импульсное входное воздействие, страница 3

p₁ = -α₁; p₂= -α₂.;

тогда уравнение (6) будет иметь вид . Прибавив к нему частное решение получим:

Так как  по подаче входной величины система находилась в равновесии, то при t = 0, y = 0, , следовательно, для начальных условий находим:

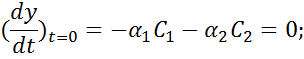
Решив систему получим:

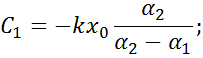
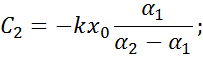
Переходный процесс при     определяется выражением:

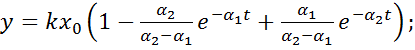
Если   

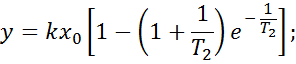
Если  

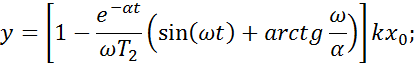
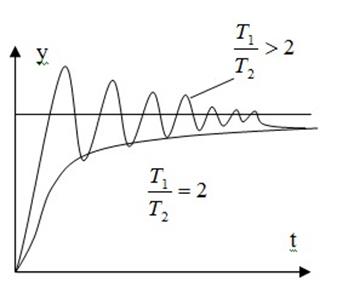
Выражение для переходного определяет собой затухающую синусоиду с убыванием амплитуды по экспоненте, определяемой величиной  . В связи с этим инерционное звено второго порядка, характеристическое уравнение которого имеет комплексные сопряженные корни называется колебательным звеном. Если корни вещественные, отрицательные, то звено называется апериодическое второго порядка.

Частотные характеристики звеньев САУ.

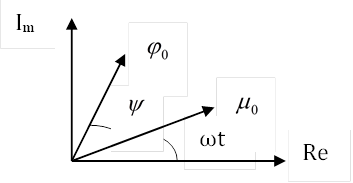
Комплексное число и его представление на плоскости.

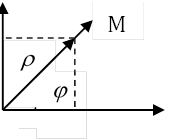1. полярная форма:

М()

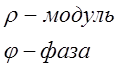
2. показательная М =;

3. комплексная, тригонометрическая форма М =;

4. алгебраическая форма М = a+jb = Re+jI_m ;

Формулы Эйлера (формулы связи).

;           

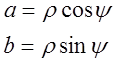
M;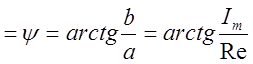

Если на вход звена или системы подавать синусоидальные колебания с постоянной амплитудой и частотой  то после затухания переходных процессов на выходе также возникает синусоидальные колебания  с той же частотой, но с другой амплитудой и сдвинутые по фазе относительно входных колебаний на угол  (амплитуда входных колебаний, амплитуда выходных колебаний, круговая частота, отставание выходного сигнала относительно входного). На комплексной плоскости входная величина  для каждого значения времени t₁ определяется вектором , проведенного из начала координат под углом .

Рассмотрим реакцию линейного звена на гармоническое возмущение при условии, что корни характеристического уравнения звена отрицательные, то есть переходный процесс, зависящий от общего решения однородного дифференциального уравнения является затухающим. Таким образом можем записать действительную и мнимую части гармонической входной величины:

тогда гармоническое возмущение в комплексной тригонометрической форме запишется в виде: .

Используя формулы Эйлера запишем входную величину в комплексной показательной форме:

по аналогии выходная величина:

Учитывая  смещение:

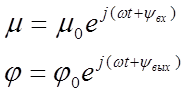
Запишем дифференциальное уравнение звена в операторной форме:

        (1);

Подставим в уравнение (1) значение выходных и входных величин, причем при подстановке гармонических функций заменим оператор p на jω:

       (2);

Из равнения (2) определим передаточную функцию звена.

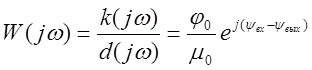                 (3)

Отношение выходной величины системы (или звена) к входной величине называется амплитудо-фазовой характеристикой системы. Модуль амплитудо-фазовой характеристики системы или отношение амплитуды выхода и входа величин функции их частоты , называется амплитудо-частотной характеристикой системы.

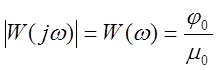
Зависимость разности фаз входных и выходных колебаний от частоты называется фазо-частотной характеристикой звена и является аргументом амплитудо-фазовой характеристики. Амплитудо-фазовая характеристики не зависит от времени, в этом заключается ее отличие от переходной функции (временной характеристики) h(t).

Если временная характеристика определяет поведение системы в переходном процессе, то АФХ выражает зависимость параметров установившихся выходных колебаний от тех же параметров входных колебаний при различных частотах. Хотя АФХ отображает только установившиеся процессы в системе она вполне определяет ее и динамические свойства, подобно временной характеристике и дифференциальному уравнению.

Дифференциальное уравнение САУ в общем случае имеет вид:

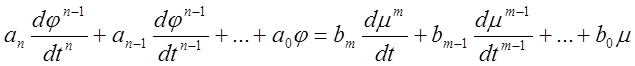         (4)

где  и - выходная и входная величины звена в отношениях от состояния звена, а_n и b_m – постоянные коэффициенты, определяемые конструктивными особенностями и параметрами настойки звена.

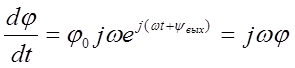
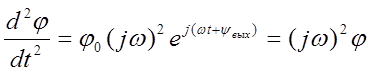
Учитывая это перепишем выражение (4):

                (5)

Из выражения (5) определим АФХ системы:

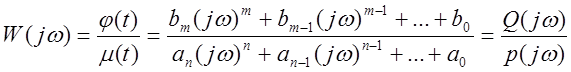                     (6)

Перепишем выражение (6) в операторной форме:

      (7)