Передаточные функции системы автоматического управления. Типовые воздействия в автоматике переходная характеристика звена. Импульсное входное воздействие, страница 2

g(p) = W(p)        (3)

Выражение (3) показывает связь функции веса с передаточной функцией.

Правило определения W – функции при подаче импульсного воздействия.

1) Подать на вход ударное воздействие.

2) Определить реакцию звена на ударную функцию, то есть получить g(t) функцию веса.

3) Определить по таблице преобразования Лапласа изображение функции веса, она и будет передаточной функцией звена.

Функции веса звена может быть определена по переходной функции:

W(p ) = h(p)∙p

g(p) = h(p)p        (4)  [вывод формулы самостоятельно]

g(t) =    (5)

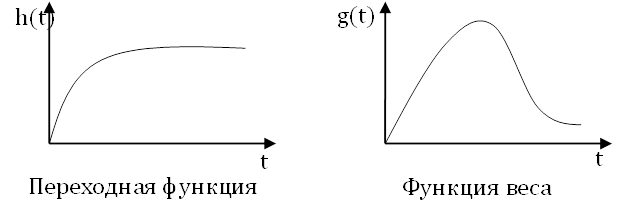Таким образом, функция веса определяется скоростью изменения передаточной функции.

Стандартные звенья

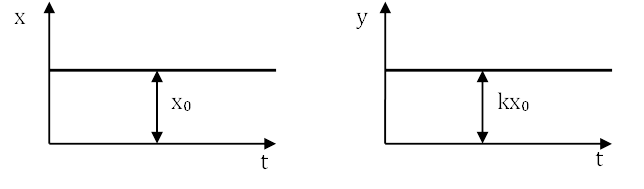
1) Безинерционное звено y(t) = kx(t).

При подаче на его вход скачкообразной входной величины получаем на выходе мгновенное изменение выходного сигнала без динамических переходных процессов и искажений.

2) Интегрирующее звено

= kx;

W(p) = ;

Определим характер изменения входной величины звена при подаче на его вход постоянной входной величины:

X(p) =;

y(p) = W(p)∙x(p);

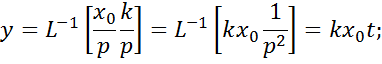
3) Инерционное звено 1-го порядка

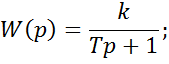
Характер изменения выходной величины при подаче на его вход скачка входной величины x₀ и найдем изображение по Лапласу от входной величины:

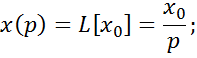
y(p) = W(p)x(p) =

Выразим оригинал функции выходной величины через его изображение

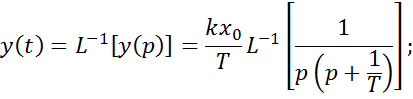
Пусть , тогда:

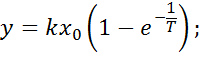
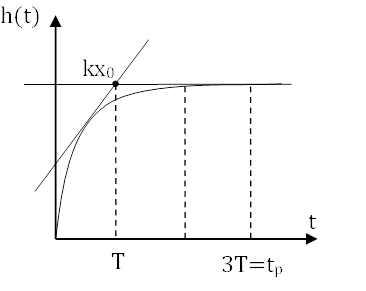
то есть кривая переходного процесса имеет вид экспоненты.

Постоянная времени t определяет динамические свойства звена, то есть чем больше T, тем медленнее протекает переходной процесс.

Примечание:время регулирования, то есть время, в течение которого выходная величина практически будет равна новому установившемуся значению (y = 0,95 kx₀), равно приблизительно 3T . По степени этого времени динамическая ошибка регулирования составляет всего 5% нового установившегося значения выходной величины. Постоянная времени звена определяется как проекция на ось времени отрезка касательной к экспоненте, заключенного между точкой касания и точкой пересечения касательной с линией установившегося значения выходной величины:

4) Дифференцирующее звено.

W(p)=kp

Подача x₀ на вход дифференцирующего звена должна вызвать мгновенное изменение выходной величины от 0 до ∞ и немедленный спад ее до 0, что практически невозможно. Поэтому рассмотрим реальное дифференцирующее звено:

Изображение выходной величины при скачкообразном изменении входной от 0 до x₀ будет иметь вид:

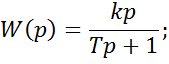
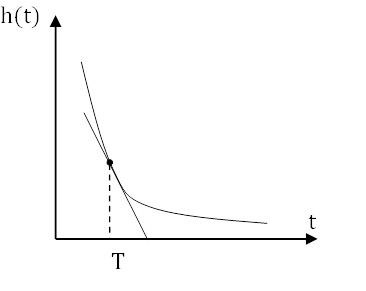5) Инерционное звено 2-го порядка.

         (1)

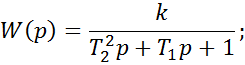
Переходный процесс инерционного звена 2-го порядка исследуем путем решения дифференциального уравнения (1);

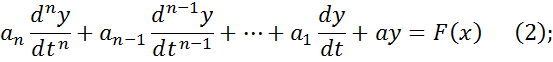
Для получения общего решения неоднородного уравнения (2) при скачкообразном изменении входной величины достаточно получить какой либо частное его решение, плюс решение общего вида, то есть уравнение (2) с нулевой правой частью. Одно из частных решений при x = x₀ будет новое значение x₀ установившееся после окончания переходного процесса

x = x₀;

a₀y = F(x)      (3);

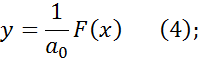
Однородное дифференциальное уравнение, полученное из уравнения (2) при F(x) = 0 и запишем его характеристическое уравнение:

a_npⁿ + a_n-1p^n-1 + … + a₁p+а₀ = 0        (5);

Определим корни характеристического уравнения и запишем общее решение однородного дифференциального уравнения:

Характеристическое уравнение (6) в общем случае может иметь i-одинаковых корней и

С и А – постоянные интегрирования, которые находятся из начальных условий.

Описанный метод решения дифференциальных уравнений может использоваться для исследования переходных процессов всех раннее рассмотренных звеньев. Характеристическое уравнение инерционного звена 2-го порядка имеет вид:

T₂² p² + T₁p+1 = 0         (7);

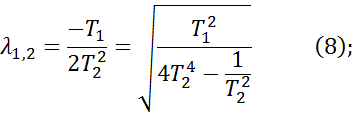
а частное решение:

Характер переходного процесса инерционного звена 2-го порядка зависит от знака подкоренного выражения формулы (8). Здесь возможно 2 случая:

1), то есть оба корня характеристического уравнения вещественные отрицательные,