Передаточные функции системы автоматического управления. Типовые воздействия в автоматике переходная характеристика звена. Импульсное входное воздействие, страница 4

Получим из (7) передаточную функцию:

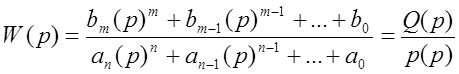     (8)

Сравним (6) и (8). Для получения АФХ системы или звена достаточно в выражении передаточной функции заменить символ p на jω.

Рассмотрим полиномы Q(jω) и P(jω):

   (9)

Выразим действительные и мнимые части:

,             

Таким образом полиномы представляют собой комплексные числа с реальными и мнимыми частями. Тогда АФХ можно записать:

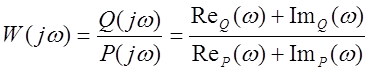         (10)

Домножим числитель и знаменатель на сопряженный множитель, получим:

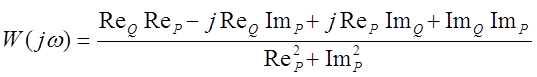
Выделим действительную и мнимую части:

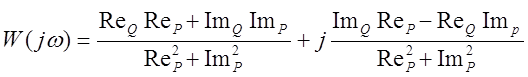    (11)

Таким образом получим:

        (12)

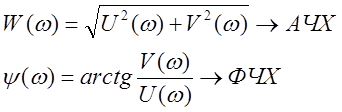(13)

(14)

Используя выражения (13) и (14) при изменении частоты от -∞ до +∞ строится графическое изображение АФХ на комплексной плоскости в координатах U(ω) и V(ω).

Очевидно, что вещественная часть АФХ является четной функцией, так как ω входит в числитель и знаменатель только в четных степенях. Таким образом, точки АФХ, соответствующие значению ω и – ω имеют одну и ту же абсциссу и разные по знаку ординаты. Следовательно АФХ симметрична относительно действительной оси и достаточно построить ее только для значения от 0 до ∞, так как другая ветвь характеристики от -∞ до 0 является зеркальным отображением построенной части относительно действительной оси.

АФХ называется годографом вектора, изображающего на комплексной плоскости частотно-передаточную функцию W(j ω) при изменении частоты от 0 до ∞. Длина вектора, проведенного из начала координат в точку АФХ соответствующей частоте равна модулю частотной передаточной функции и показывает отношение амплитуд выходного и входного сигналов, изменяющихся с частотой ω. Угол между вектором и положительной вещественной полуосью, отсчитываемой против часовой стрелки, равен аргументу частотной передаточной функции при частоте ω, и показывает сдвиг фаз выходного и входного сигналов звена при этой частоте.

Устойчивость систем автоматического регулирования

Наиболее важными динамическими свойствами системы являются: устойчивость, время регулирования, время перерегулирования, число колебаний регулируемой величины. Основная характеристика: устойчивость, т.к. три последних требования могут измениться в зависимости от назначения и условий работы установки, а требования устойчивости должно удовлетворять САУ. В зависимости от характера переходного процесса линеаризованной системы различают три основных случая поведения системы после возмущающего воздействия:

1) система не может восстановить равновесное состояние, значения управляемой переменной (выходной величины) все больше откланяется от заданного, такой процесс называется расходящимся, а система неустойчивой;

2) Система возвращается в равновесное состояние значение управляемой переменной отличается от заданного на величину статической ошибки, такой процесс называется сходящимся, а система устойчивой;

3) Система характеризуется установившимся периодическим движением, такой процесс называется колебательным, а система будет находиться на границе асимптотической устойчивости.

Методы определения устойчивости

Устойчивость линейных систем не зависит от величины возмущения. Система устойчивая при малых возмущениях, будет устойчивой и при больших возмущениях, поэтому достаточно исследовать и определить устойчивость в малом, т.е. найти устойчивость уравнением в форме приращений. Допустим, что в установившемся состоянии регулируемая величина имеет некоторое значение x₀. Выведем систему из этого состояния при помощи какого-либо воздействия, так чтобы x₀ изменилась на . И после этого устраним причину, вызвавшую это изменение, тогда система будет устойчивой, если будет выполняться условие:

      (1)