В случае невыполнения этого условия, система будет неустойчивой. Допустим, что изменение регулируемой величины в процессе регулирования. Описывается линейным уравнением n-го порядка с постоянными коэффициентами, тогда отклонение ∆x также будет описываться дифференциальным уравнением этого порядка. Интегрируя полученное уравнение, находим закон изменения интересующей нас переменной по времени, согласно которому можно сделать заключение о характере переходного процесса (устойчивый, неустойчивый). Устойчивость системы определяют характером свободного движения системы, так как свободное движение системы описывается однородным дифференциальным уравнением (без правой части), то для нахождения условий устойчивости достаточно исследовать свойства решения однородного дифференциального уравнения. В общем случае для системы n-го порядка имеем дифференциальное уравнение, которое описывает поведение отклонения ∆x регулируемой величины:
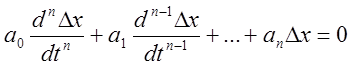 (2)
(2)
а0, а1, аn- постоянные коэффициенты, величина которых зависит от параметров САУ.
Решение (2) может быть представлено в виде:
![]() =
=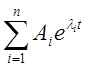 (3)
(3)
Ai- постоянная интегрирования, определяется из начальных условий.
![]() - корни,
характеризующие свободное движение и определяемые из характеристического
уравнения.
- корни,
характеризующие свободное движение и определяемые из характеристического
уравнения.
![]()
Исследуем
(3) с точки зрения устойчивости системы, согласно определению для устойчивости
системы необходимо, чтобы отклонение ![]() при t
при t![]() , а это возможно только тогда, когда все
составляющие уравнения (3) с течением времени стремятся к 0. Поскольку все Ai=const, то следовательно
характер поведения каждой составляющей
, а это возможно только тогда, когда все
составляющие уравнения (3) с течением времени стремятся к 0. Поскольку все Ai=const, то следовательно
характер поведения каждой составляющей ![]() зависит от
зависит от ![]() . Если
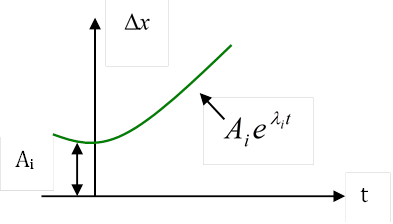
. Если ![]() - положительное, вещественное число, то
составляющая
- положительное, вещественное число, то
составляющая ![]() будет
увеличиваться до бесконечности.
будет
увеличиваться до бесконечности.
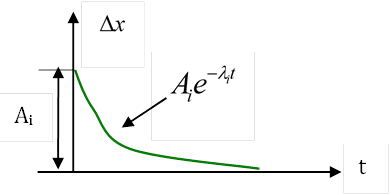
При
отрицательных вещественных корнях составляющая свободного движения при t![]() монотонно убывает до 0.
монотонно убывает до 0.
 |
|||
 |
|||
![]() - комплексное число,
тогда выражение
- комплексное число,
тогда выражение ![]() запишется
запишется
![]()
![]() (5) – это
колебательный процесс, амплитуда А которого возрастает или убывает в
зависимости от знака вещественной части
(5) – это
колебательный процесс, амплитуда А которого возрастает или убывает в
зависимости от знака вещественной части ![]() комплексного корня. Если
комплексного корня. Если ![]() >0, то получим колебательный процесс
с нарастающей амплитудой. Если
>0, то получим колебательный процесс
с нарастающей амплитудой. Если![]() <0, то при t
<0, то при t![]() , А
, А![]() .
.
Т.о. аналитические выражения составляющих свободного движения имеют вид:
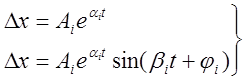 (6)
(6)
Ai-постоянная интегрирования, определяется из начальных условий.
![]() - вещественная часть корня,
характеризующая интенсивность затухания колебаний.
- вещественная часть корня,
характеризующая интенсивность затухания колебаний.
![]() - мнимая часть корня,
хар-ся частоту свободных колебаний.
- мнимая часть корня,
хар-ся частоту свободных колебаний.
![]() - начальная фаза.
- начальная фаза.
Условие устойчивости
Чтобы САУ описываемая линейными диф.ур. с постоянными коэффициентами была устойчивой, необходимо и достаточно, чтобы вещественные корни диф.ур. были отрицательны, а комплексные корни имеем отрицательную вещественную часть.
Устойчивость линеаризованных систем
Система автоматического управления описывается нелинейными дифференциальными уравнениями, однако при малых отклонениях регулируемой величины в большинстве случаев нелинейную систему можно заменить ее линейной моделью, и исследовать нелинейную систему как линеаризованную, это доказывает теорема Ляпунова.
Теорема Ляпунова.
1. Если характеристическое уравнение линеаризованной системы имеет все корни с отрицательными вещественными частями, то исходная система, описанная линейными уравнениями, - устойчива, при этом никакие отброшенные при линеаризации члены 2-й и высших степеней не могут изменить устойчивости системы.
2. Если характеристическое уравнение линеаризованной системы имеет хотя бы один корень с положительной вещественной частью, то исходная система неустойчива, при этом никакие отброшенные при линеаризации 2-й и высшей степеней отклонения переменной не могут придать системе устойчивость.
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.