Передаточные функции системы автоматического управления. Типовые воздействия в автоматике переходная характеристика звена. Импульсное входное воздействие, страница 9

Таким образом, система устойчива, если изменения аргумента вектора F(jω) при изменении частоты от 0 до ∞, равном нулю.

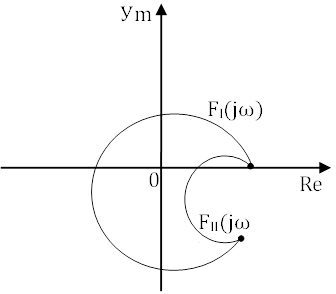
Годограф F_I(jω) неустойчивая система, так как охватывает точку (0;0). Годограф F_II(jω) – устойчивая система, так как не охватывает точку (0;0).

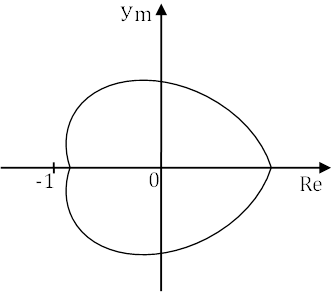
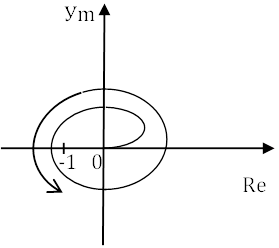
Передаточная функция разомкнутой системы от W(jω) отличается от F(jω) на -1, то есть непосредственно для характеристики  W_{разомкнутое}(jω) критерий Найквиста формулируется: если система устойчива в разомкнутом состоянии, то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы для частоты, изменяющейся от 0 до ∞ не охватывало точку с координатами (-1j, 0).

Случай 2: система в разомкнутом состоянии неустойчива. В этом случае характеристическое уравнение разомкнутой системы имеет m корней в правой полуплоскости. Согласно принципу аргумента можем записать ∆argD(jω)_{при-∞<ω<∞} =(n – 2m)π (5). Учитывая симметрию характеристики перепишем (5): ∆argD(jω)_{при 0<ω<∞} =(n – 2m) (6). То есть для устойчивости системы в замкнутом состоянии необходимо, чтобы выполнялось равенство ∆arg(D(jω)+K(jω))_{при 0<ω<∞} = n (7).

При изменении аргумента функции F(jω) должно выполняться выражение:

ΔargF(jω)_{при0<ω<∞}  = Δarg(D(jω)+K(jω))_{при0<ω<∞} - ΔargD(jω)_{при0<ω<∞} = n - (n-2m) = 2π (8);

Таким образом, система автоматического управления устойчивая, если при изменении частоты от 0 до ∞ годограф разомкнутой системы W_раз(jω) охватывает  раз точку (-1,j₀) в положительном направлении. m –число корней характеристического уравнения разомкнутой системы лежащих в правой полуплоскости.

Влияние параметров системы на ее устойчивость.

Рассмотрение влияния параметров системы на ее устойчивость может производиться путем анализа числа корней характеристического уравнения, лежащих в правой полуплоскости пространства параметров системы. Этот метод называется D-разбиение пространства параметров и представляет собой критерий устойчивости, обобщающий все рассмотренные выше критерии устойчивости, дающий возможность построения кривой, по которой можно определить все те значения интересующего нас параметра, при которой система остается устойчивой.

Пусть дано характеристическое уравнение n-степени:

A(p) = apⁿ + a_n-1p^n-1 +…+a₀ (1)

При заданном значении коэффициентов уравнения, в общем случае, оно имеет m – корней в правой полуплоскости, и n – m левая полуплоскость. При изменении коэффициентов уравнения, корни его также изменяются и, следовательно, перемещаются в плоскости корней, описывая определенную кривую. При некотором значении коэффициентов, один из действительных корней характеристического уравнения попадает на мнимую ось и становится равным нулю. А при выходе на мнимую ось двух комплексных сопряженных корней  характеристического уравнения имеется два чисто мнимых корня. Значения всех этих коэффициентов должно удовлетворять уравнению :

A(jω) = a_n(jω)ⁿ + a_n-1(jω)^n-1 +…+a₀ = 0 (1);

Уравнение (2) в (n-1)-мерном пространстве коэффициентов, по осям которого отложены коэффициенты a₀, a₁, … a_n , описывает точку при данном значении частоты.

p³+a₂p²+a₁p+a₀=0 (3);

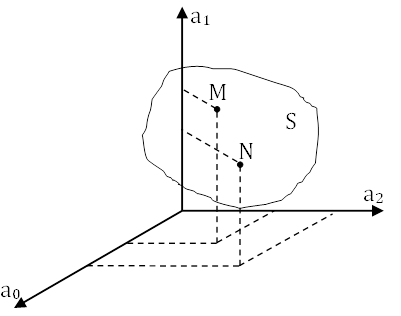
При изменении частоты от -∞ до +∞ получим поверхность S на которой выполняются условия A(jω)=0 и следовательно пара или один корень будет переходить из правой или левой полуплоскости корней в левую или правую полуплоскость.

Для уравнения (3) распределение корней будет выглядеть:

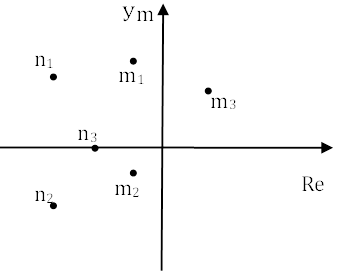Для точки M(m₁,m₂,m₃); N(n₁,n_2­,n₃).

При некотором значении коэффициентов некоторые корни окажутся на мнимой оси, то есть будут иметь вид (, следовательно, соответствующая точка в пространстве будет удовлетворять уравнению: (jω)³+a₂(jω)²+a₁(jω)+a₀=0 (4).