Передаточные функции системы автоматического управления. Типовые воздействия в автоматике переходная характеристика звена. Импульсное входное воздействие, страница 10

К этому уравнению, при изменении частоты от -∞ до +∞ соответствует поверхность S в пространстве коэффициентов. При изменении коэффициентов характеристического уравнения его корни изменяются и попадают на мнимую ось только тогда, когда точка в пространстве коэффициентов попадает на поверхность S. При пересечении точкой поверхности корни переходят из одной полуплоскости в другую. Следовательно, поверхность S разделяет пространство коэффициентов на области, каждой точке которой соответствует полином 3-ей степени (в данном случае), имеющий определенное количество корней в правой и левой части плоскости корней.

Введем обозначение, если характеристический полином n-ной степени имеет m корней справа, и n-m слева от мнимой оси, то всю область пространства можно записать D(n-m,m). Например, D(3,0) – область устойчивости, так как все три корня находятся слева от мнимой оси.

Переход через границу D-разбиений соответствует переходу корней уравнения через мнимую ось, поэтому уравнение границы D-разбиения имеет вид уравнения (2) и может быть получено из характеристического уравнения заменой p на jω. По полученной форме уравнения можно построит границу D-разбиения, где частота изменяется от -∞ до +∞. Аналогично, можно построить D-разбиение в пространстве не коэффициентов уравнения, а параметров системы, от которых зависят коэффициенты характеристического уравнения.

D-разбиение плоскости одного комплексного числа.

Если требуется выяснить значение одного параметра, а значение остальных параметров заданы, следует ввести вместо этого параметра комплексную величину, вещественная часть которой равна исследуемому параметру.

Пусть τ - коэффициент, влияние которого определяется. Предположим, что τ входит линейно в характеристическое уравнение A(p)=P(p)+τQ(p) (1). Граница D-разбиения определяется выражением A(jω)=P(jω)+τD(jω) (2).

τ представлена комплексным числом, это позволяет в результате подстановки p вместо jω отобразить мнимую ось, в плоскости корней, на плоскость комплексного коэффициента τ. После этого можно мнимую часть отделить от вещественной: τ= τ(jω)=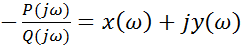 (3).

Придавая различные значения ω строим кривую, которая отображает мнимую ось комплексной плоскости, то есть границу D-разбиения плоскости τ(jω). В связи с симметричной частью характеристик, относительно вещественной оси достаточно построить кривую D-разбиений для частоты от 0 до ∞, а затем дополнить ее зеркальным отображением относительно вещественной оси. Нас интересует D-разбиение не всей комплексной плоскости, а лишь ее действительные оси, которым отвечают действительные значения коэффициента τ.

Отображение  мнимой оси комплексной плоскости корней p и есть кривая D-разбиения на комплексной плоскости параметра τ, которой вся область плоскости τ разбивается на области.

Для всех τ лежащих внутри каждой области все полиномы будут иметь одинаковое число корней слева от мнимой оси.

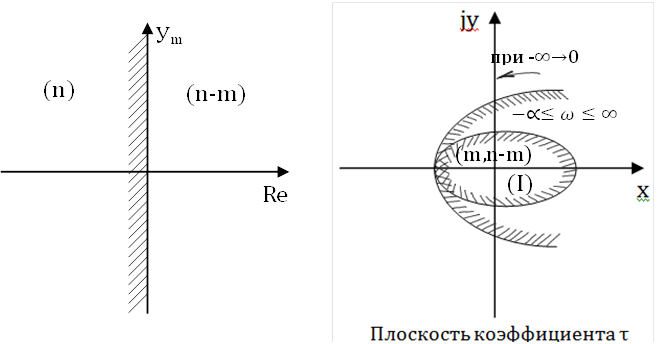
После того, как найдена граница D-разбиений, необходимо наметить предполагаемую область устойчивости, для этого определим в какой области количество корней слева от мнимой оси наибольшее, для этого применяют правило штриховки Неймарка: при изменении частоты от -∞ до +∞ в плоскости P мнимая ось проходит снизу-вверх, при этом левая полуплоскость остается слева. Такому движению по мнимой оси соответствует движение по границе D-разбиения области τ, которую штрихуют слева по обходу при изменении частоты от -∞ до +∞. (В MathCAD можно строить, но нужно задавать таблицу значений).

Тогда при переходе через кривую с заштрихованной стороны на не заштрихованную теряется корень слева от мнимой оси. Если штриховка двойная то мнимую ось пересекает 2 корня, таким образом часть плоскости, в сторону которой направлены штрихи является отображением левой полуплоскости корней и может рассматриваться как предполагаемая область устойчивости. Так как коэффициент τ вещественная величина, то рассматриваются лишь те отрезки вещественной оси, которые лежат в области окруженной внутренней штриховкой.