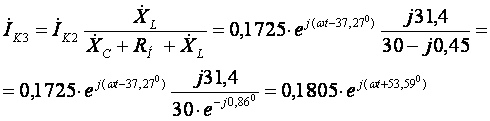Пособие по выполнению расчётно-графической работы по курсу «Общая электротехника и электроника», страница 9

              .

В алгебраической форме ток   имеет вид:

                                .  

После определения контурных токов переходим к определению токов в ветвях. В соответствии с методом расчёта токи в собственных ветвях контуров равны контурным токам этих контуров. В соответствии с этим находим токи  и :

 

        

Токи в общих ветвях определяются как алгебраическая сумма контурных токов, протекающих через эти ветви. Ток  равен разности контурных токов  и , так как они протекают через эту ветвь в противоположные стороны:

                      

Подставляем численные значения контурных токов    и  в алгебраической форме и находим значение тока   в алгебраической и показательной форме:

                                                          

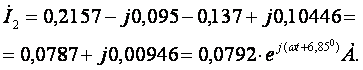
Ток  равен разности контурных токов  и , так как они протекают через эту ветвь в противоположные стороны:

                      

Подставляем численные значения контурных токов    и  в алгебраической форме и находим значение тока   в алгебраической и показательной форме:

                

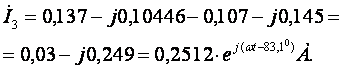
Находим напряжения на элементах:

 В.

В.

 В.

 В.

Определим погрешность выполненного расчёта. В начале определим мощность, выделяемую источником:

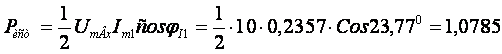       Вт.

Далее определим мощность, потребляемую диссипативными элементами схемы по известной формуле:

.

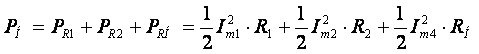Подставляя численные значения найденных токов, находим:

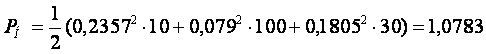  Вт.

Погрешность определяем по известной формуле:

                       .

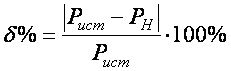Подставляем найденные значения мощностей:

           .

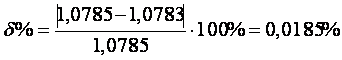Как видим, точность расчёта этим методом выше точности расчёта предыдущих методов и на порядок выше точности расчёта с помощью законов Кирхгофа. Недостатком этого метода является меньшая наглядность по сравнению с другими методами. Воспользоваться рекомендациями приложения 2 в нём можно только после определения всех токов в ветвях.

Наибольшею наглядностью обладает метод эквивалентного преобразования. В нём видно как формируется полное сопротивление цепи, которое определяет входной ток и как этот ток далее распределяется по ветвям.