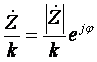Пособие по выполнению расчётно-графической работы по курсу «Общая электротехника и электроника», страница 13

                                        .                                      (10)

          При делении комплексного числа на отрицательное число () модуль его изменяется так же, как в предыдущем случае, но так же изменяется  и его фаза на .

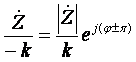                                         .                              (11)

 При делении комплексных чисел они должны быть представлены в показательной форме (2). В процессе деления модуль числителя делится на модуль знаменателя, а фаза результирующего числа равна разности фаз числителя и знаменателя:

                                        .                        (12)

Извлечение корня из комплексного числа.

   При необходимости извлечения квадратного корня из комплексного числа необходимо подкоренное выражение представить в показательной форме (2). В результате извлекается квадратный корень из модуля, а фаза делится на два:

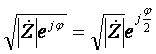                            .                         (13)

Умножение и деление комплексного числа на мнимую единицу.

    В соответствии с теорией функций комплексного переменного, умножение комплексного числа на мнимую единицу  эквивалентно изменению его фазы на . Это значит, что если в комплексном выражении, представленном в показательной форме (2), есть мнимая единица в виде сомножителя, то она может быть отброшена, а в место неё фаза изменена на угол .

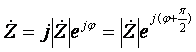                                                (14)

       Деление комплексного числа на мнимую единицу эквивалентно изменению его фазы на . Это значит, что если в комплексном выражении, представленном в показательной форме, есть мнимая единица в виде делителя, то она может быть отброшена, а в место неё фаза изменена на .

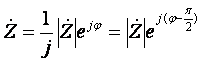                 .                         (15)

Переход от комплексного числа в виде дроби к комплексному числу в алгебраической форме.

  При расчётах часто встречается комплексное выражение в виде дроби

                                        ,

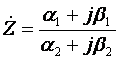которое необходимо представить в алгебраической форме. Решение этой задачи можно выполнить двумя путями. Первый состоит в том, что числитель и знаменатель представляют в показательной форме (2), затем выполняется операция деления комплексных чисел (12), которая даёт результат в показательной форме (2). Для достижения конечного результата необходимо полученное выражение перевести в алгебраическую форму, пользуясь формулами (3) и (4).

          Второй способ состоит в умножении знаменателя и числителя на комплексно-сопряжённое знаменателю число. Знаменатель становится вещественным числом, а в числителе выполняется перемножение комплексных чисел и группировка вещественных и комплексных составляющих. Далее деление вещественной составляющей на знаменатель даёт вещественную составляющую, а деление мнимой составляющей на знаменатель даёт мнимую составляющую комплексного числа.