Пособие по выполнению расчётно-графической работы по курсу «Общая электротехника и электроника», страница 6

       С учётом сказанного, в схеме только два узла, а в качестве независимого узла выберем верхний распределённый узел и для него, в дальнейшем будет записано уравнение по первому закону Кирхгофа.

       В схеме три независимых контура. Выбираем контура, содержащие такие элементы:   ,  . Для каждого контура составляются уравнения по второму закону Кирхгофа. Все составленные уравнения образуют следующую систему уравнений (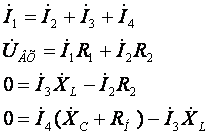5)                

                                  (5)         

    Расчёт системы можно проводить методом Крамара или методом последовательного исключения. Воспользуемся методом последовательного исключения. Подставим первое уравнение системы во второе уравнение. После эквивалентного преобразования система принимает вид 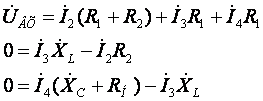(6):

                      (6)

Из третьего уравнения системы (6) находим ток:

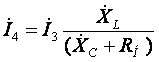                     .                     (7)

Подставляем найденный ток (7) в первое уравнение системы (6) и после эквивалентного преобразования система принимает вид 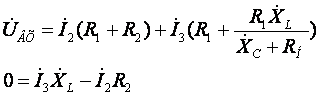(8):

             .                 (8)

Из второго уравнения системы (8) находим ток :

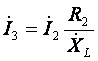                    .                             (9)

Подставляем найденный ток  (9)  в первое уравнение системы (8) и после эквивалентных преобразований, получаем:

            .

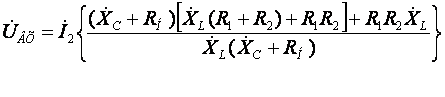
  Решаем полеченное уравнение относительно тока :

          .

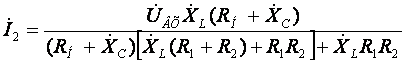В полученное выражение  подставляем численные значения:

     .

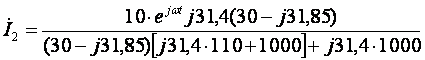Осуществляя необходимые преобразования, получаем решение для  в показательной и алгебраической форме:

                        А.                    (10)

 Ток находим по формуле (9), подставляя в неё численные значения:

                 .

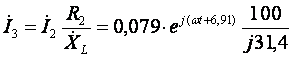После необходимых преобразований находим значение тока в показательной и алгебраической форме:

                      А.                  (11)

Ток находим по формуле (7), подставляя в неё численные значения:

                   .

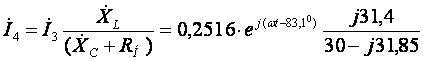После необходимых преобразований находим значение тока в показательной и алгебраической форме:

              А.             (12)

Ток находим в соответствии с первым законом Кирхгофа по формуле:

                                     

Подставляем в это выражение значения токов в алгебраической форме (10), (11), (12) и, суммируя вещественные и мнимые составляющие, находим в начале ток в алгебраической форме, а потом и в показательной: