Пособие по выполнению расчётно-графической работы по курсу «Общая электротехника и электроника», страница 5

Входное напряжение:

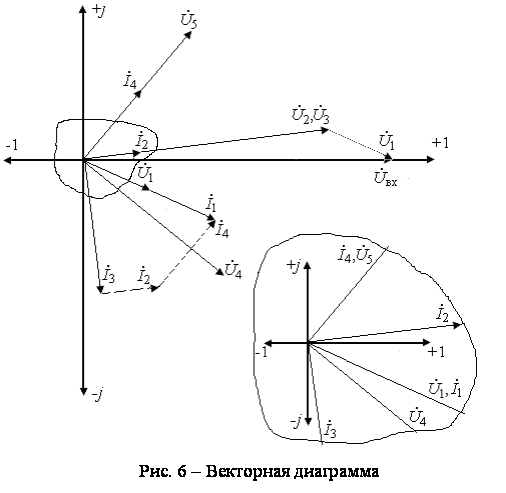
Построение векторной диаграммы следует выполнять в соответствии с требованиями, изложенными в приложении 2.

   Векторная диаграмма представлена на рис.6.

 

 

 На этом расчёт электрической цепи заканчивается.

       5. Расчёт электрической цепи с помощью законов Кирхгофа.

  Прежде чем приступить к расчёту названным методом, рассмотрим основные положения этого метода и последовательность расчёта этим методом в соответствии  .

При расчете этим методом первоначально определяются токи в ветвях, а затем напряжения на всех элементах. Токи находятся из уравнений, полученных с помощью законов Кирхгофа. Так как в каждой ветви цепи протекает свой ток, то число исходных уравнений должно равняться числу ветвей цепи. Число ветвей принято обозначать через n. Часть этих уравнений записываются по первому закону Кирхгофа, а часть - по второму закону Кирхгофа. Все полученные уравнения должны быть независимыми. Это значит, чтобы не было таких уравнений, которые могут быть получены путем перестановок членов в уже имеющемся уравнении или путем арифметических действий между исходными уравнениями. При составлении уравнений используются понятия независимых и зависимых узлов и контуров.

Независимым узлом называется узел, в который входит хотя бы одна ветвь, не входящая в другие узлы. Если число узлов обозначим через К, то число независимых узлов равно (К-1).

Независимым контуром называется контур, который отличается от других контуров хотя бы одной ветвью, не входящей в другие контура. В противном случае такой контур называется зависимым.

    Если число ветвей цепи равно n, то число независимых контуров равно

 [n-(К-1)].

Последовательность расчёта:

1. Расставляем условно – положительные направления токов и напряжений.

2. Определяем число неизвестных токов, которое равно числу ветвей (n).

3. Определяем число независимых узлов и контуров и выбираем их на схеме.

4. С помощью первого закона Кирхгофа составляем (К–1) уравнений для независимых узлов.

5. С помощью второго закона Кирхгофа составляем [n – (К–1)] уравнений для независимых контуров. При этом напряжения на элементах выражаются через токи, протекающие через них.

6. Решаем составленную систему уравнений и определяем токи в ветвях. При получении отрицательных значений для некоторых токов, необходимо их направления в схеме изменить на противоположные, которые и являются истинными.

7. Определяем падения напряжений на всех элементах схемы.

   В соответствии с рассмотренной последовательностью расчёта, расставляем на схеме условно-положительные направления токов и напряжений. Это уже было сделано и показано на рис.3, поэтому воспользуемся этой схемой и повторим её 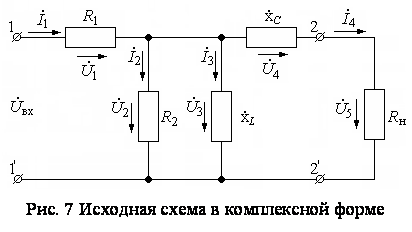на рис.7.

         На схеме две ветви, содержащие  и , включены параллельно и у них должны быть общие узлы с обеих сторон соединения. Однако, на схеме каждая ветвь имеет свой узел, между которыми находится перемычка. Такие узлы принято называть распределёнными и на схеме они воспринимаются за один узел. В схеме в этих случаях токи в перемычках не представляют интерес и они не определяются. Исходя из сказанного, в схеме имеется четыре ветви, а значит в схеме четыре неизвестных тока.