Пособие по выполнению расчётно-графической работы по курсу «Общая электротехника и электроника», страница 11

 7. Могут иметь место случаи, когда значения токов или напряжений сильно отличаются по величине, т.е. имеются достаточно большие значения тока и не значительные. Тогда вектор малой величины имеет малый размер и по нему трудно судить о его направлении, в этом случае необходимо сделать вынос этого участка векторной диаграммы на этом же или на отдельном листе. Для этого на основной векторной диаграмме произвольно показывается граница выносимой части, а затем такая же граница показывается на вынесенной части. На вынесенной части берется более крупный масштаб для токов и напряжений. Это приводит к тому, что вектор малых размеров становится различимым и будет видно его фазовое положение относительно других векторов, а остальные вектора будут выходить за границы этой векторной диаграммы. В качестве примера на рис.6 показано как это выполняется относительно тока , хотя в данном примере в этом нет необходимости, т.к. этот вектор хорошо просматривается на основной векторной диаграмме.

                                                                                      Приложение 3

            КОМПЛЕКСНЫЕ ВЕЛИЧИНЫ И ДЕЙСТВИЯ НАД НИМИ

             При анализе электрических и радиотехнических цепей ши­роко используются комплексные величины. Рассмотрим ос­новные сведения о комплексных величинах.

    Комплексное число  имеет следующие формы представления: алгебраи­ческую, показательную, геометрическую и тригонометричес­кую.

   Алгебраическая форма представления комплексного числа:

                                 ,                                            (1)

где  - вещественная составляющая, - мнимая составляющая комплексного числа.

    Комплексное число в показательной форме имеет вид:

                            ,                                               (2)

       где                 -  модуль комплексного числа,

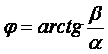                                     - фаза комплексного числа.

      Комплексное число может быть представлено в виде век­тора на комплексной плоскости (рис. 1). Под комплексной плоскостью понимается плоскость, на которой ось абсцисс являет­ся осью вещественных составляющих комплексного числа и обозначается единицей (+1), а ось ординат является осью мнимых составляющих комплексного числа и обозначается . Как видно из рис.1, вектор, соответствующий комплексному числу, характеризуется модулем и фазой, как при показатель­ной форме.

Рисунок привести в соответствии с текстом

                                           

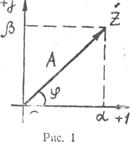
 Рис.П.1 Представление комплексного числа на комплексной плоскости

        Проекция вектора на вещественную ось комплексной плоскости равна вещественной составляющей комплексного числа в алгеб­раической форме, а проекция этого вектора на мнимую ось равна мнимой составляющей комплексного числа в алгебраи­ческой форме (1).

        Исходя из векторной диаграммы рис. 1, вытекает тригонометрическая форма представ­ления комплексного числа:

                                                                (3)

     В процессе расчётов возникает необходимость перехода из одной формы представления комплексного числа в другую. Остановимся на этих действиях. Сравнивая (2) и (3), можно сделать вывод, что из показательной формы представления комплексного числа (2) можно перейти к  тригонометрической форме (3), выполняя очевидные действия.