Пособие по выполнению расчётно-графической работы по курсу «Общая электротехника и электроника», страница 7

               А.

Находим напряжения на элементах:

 В.

В.

 В.

 В.

   Сравнивая полученные здесь результаты расчётов  с результатами предыдущего расчёта видим, что имеет место достаточно хорошее их совпадение. Однако, определим погрешность выполненного расчёта.

   Определим мощность, выделяемую источником:

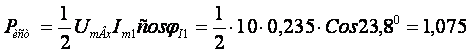       Вт.

  Определим мощность, потребляемую диссипативными элементами схемы по известной формуле:

.

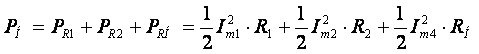Подставляя численные значения найденных токов, находим:

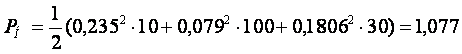  Вт.

Погрешность определяем по известной формуле:

                       .

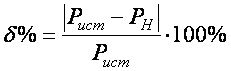Подставляем найденные значения мощностей:

           .

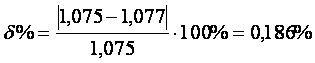Как видим, полученная погрешность удовлетворяет требованию задания.

                6. Расчёт электрической цепи методом контурных токов

   Прежде, чем приступить к рассмотрению примера расчёта схемы методом контурных токов, рассмотрим основные положения этого метода и последовательность расчёта  в соответствии с.

Сложные схемы характеризуются наличием значительного числа ветвей. В случае применения предыдущего метода это приводит к необходимости решать систему из значительного числа уравнений. Метод контурных токов позволяет уменьшить число исходных уравнений, а значит несколько облегчить расчёт.

 При расчёте методом контурных токов используются понятия не зависимого контура и зависимого контура, которые использовались в предыдущем методе. Кроме них в этом методе используются ещё следующие понятия:

- собственный элемент контура - элемент, относящийся только к одному контуру;

- общий элемент контура - элемент, относящийся к двум и более контурам цепи.

Обозначаем, как и раньше, через К число узлов, а через n число ветвей цепи. Тогда  число независимых контуров цепи определяется по уже известной формуле [n-(К-1)].

Метод основывается на предположении, что в каждом не зависимом контуре течёт собственный контурный ток, и вначале находят контурные токи в не зависимых контурах. Токи в ветвях цепи определяют через контурные токи. При этом исходят из того, что в собственных элементах контура токи совпадают с контурным током данного контура, а в общих элементах ток равен алгебраической сумме контурных токов тех контуров, к которым принадлежит данный элемент.

Последовательность расчёта:

1. Определяется число ветвей (n) и число узлов (К) цепи. Находится число независимых контуров [n-(К-1)].

2. Выбирается [n-(К-1)] не зависимых контура.

3. Выбирается  условно-положительное  направление  контурных токов в  каждом  из  независимых  контуров  (обычно  показывается стрелкой).

4. Для каждого из независимых контуров составляется уравнение по второму закону Кирхгофа. При этом падение напряжения на собственных элементах  определяется как произведение контурного тока на величину сопротивления, а на общих элементах - как произведение алгебраической суммы всех контурных токов, протекающих через данный элемент, на величину его сопротивления. Обход контура производится, как правило, в направлении собственного контурного тока.

5. Решается система из [n-(К-1)] уравнений и находятся контурные токи.

6. Токи в ветвях схемы находятся следующим образом:

- в собственных элементах контура ток равен контурному току;