Пособие по выполнению расчётно-графической работы по курсу «Общая электротехника и электроника», страница 8

- в общих элементах контура ток равен алгебраической сумме токов, протекающих через данный элемент.

Пример применения метода контурных токов при расчёте электрических цепей рассмотрим на той же схеме (рис.3) и представим её на рис.7. Как рассматривалось выше, в этой схеме три независимых контура. Тогда в каждом независимом

контуре выбираем направления контурных токов и показываем эти контурные токи.

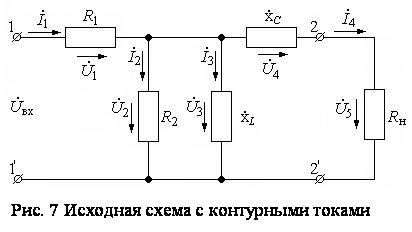
Вставить контурные токи

Для дальнейшего удобства расчёта расставим в схеме условно-положительные направления токов и напряжений. Далее, в соответствии с п.4 «последовательности расчёта», для каждого независимого контура составляем уравнения по второму закону Кирхгофа. В результате этих действий получаем систему (13) из трёх уравнений:

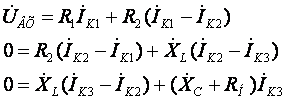                                (13)

В полученных уравнениях раскрываем скобки и приводим подобные:

                  

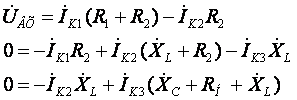     (14)

Из третьего уравнения системы (14) находим ток :

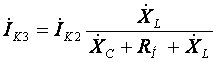                           (15)

Подставляем выражение тока   (15) во второе уравнение системы (14), в результате чего, после приведения подобных членов, эта система принимает вид:

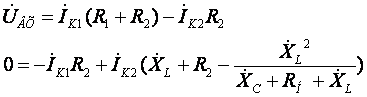                        (16)

Во втором уравнении системы (16) коэффициент  при токе  имеет довольно громоздкий вид. Для дальнейшего анализа будет удобно обозначить его какой-нибудь буквой, например , т.к. этот коэффициент имеет размерность сопротивления:

                 .                (17)

Подставим численные значения в формулу (17) и найдём значение  в алгебраической и показательной форме:

                                    (18)

С учётом (17) система уравнений (16) принимает вид:

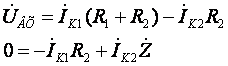                                                (19)

Из второго уравнения системы (19) найдём ток :

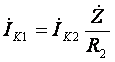                        .                                    (20)

Подставим выражение для тока  (20) в первое уравнение системы (19) и после приведения к общему знаменателю, получим:

                                 .  

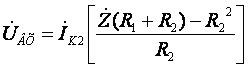Из этого уравнения находим ток  :

                      .

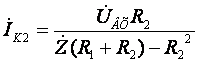В полученное выражение для тока   подставляем численные значения и находим значение тока в алгебраической и показательной форме:

                             .          (21)

Для определения тока   воспользуемся формулой (20), подставляем в неё численные значения и находим значение тока в алгебраической и показательной форме:

                   .                  (22)

Теперь определяем ток , для чего используем формулу (15). Здесь удобнее будет использовать ток  в показательной форме. Подставляем численные значения в (15) и в результате очевидных преобразований получим значение    в показательной форме: