Информатика и выч. техника \ Информатика

Основы алгоритмизации и вычислений: Учебно-практическое пособие, страница 8

3.4. Перевод из одной системы счисления в другую.

            Существует три способа перевода чисел из одной системы счисления в другую, это:

1.  Перевод с использованием формулы разложения по степени основания;

2.  Перевод целых чисел делением на основание;

3.  Поразрядные способы перевода (переводы с использованием таблиц).

3.4.1. Перевод с использованием формулы разложения по степени основания.

            В основе способа перевода лежит использование веса разрядов чисел. Перевод с использованием формулы разложения по степеням основания удобен для перевода в десятичную систему счисления, так как в процессе преобразования действия выполняются в новой системе счисления.

            Алгоритм перевода из одной системы счисления в другую представлен на рисунке 7.

            Рассмотрим процесс перевода с использованием формулы разложения по степени основания на примерах:

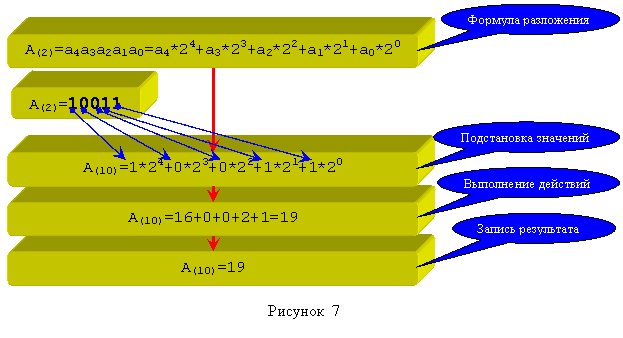
Пример 1.

Дано A(2)=10011. Найти A(10). Решение примера приведено на рисунке 7.

Пример 2.

Дано A(8)=257. Найти A(10).

Решение:

            A(8)= a2a1a0=a2*82+a1*81+a0*80

            A(10)= 2*64+5*8+7*1=128+40+7

            A(10)=175

Пример 3.

Дано A(16)=1EF6. Найти A(10).

Решение:

            A(16)= a3a2a1a0= a3*163+a2*162+a1*161+a0*160

            A(10)= 1*4096+14*256+15*16+6*1=4096+3584+240+6

            A(10)=7926

3.4.2. Перевод целых чисел делением на основание.

            Правило заключается в деление числа на основание с остатком, если остаток больше основания то он снова делиться на основание, до тех пор, пока остаток не станет меньше основания.

            При этом способе перевода действия выполняются в исходной системе счисления, поэтому это способ удобен для перевода из десятичной системы счисления в остальные системы счисления.

Пример 1.

Дано A(10)=43. Найти A(2).

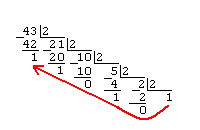
Ответ A(2)=101011

Пример 2.

Дано A(10)=132. Найти A(8).

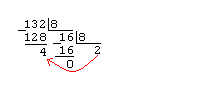
Ответ A(8)=204

Пример 3.

Дано A(10)=213. Найти A(16).

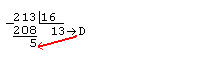
Ответ A(16)=D5

3.4.3. Поразрядные способы перевода.

            Перевод чисел упрощается, если основание старой системы счисления p и новой системы счисления q связаны отношением:

p=qk или q=pk,

            где:

                        p – основание исходной системы счисления;

                        q – основание результирующей системы счисления;

                        k – целое число.

            Для систем счисления используемых в вычислительной технике  значение k приведено в таблице 3.

Таблица 3.

Исходная система счисления

Результирующая система счисления

Значение k

Восьмеричная

Двоичная

3

Двоичная

Восьмеричная

3

Шестнадцатеричная

Двоичная

4

Двоичная

Шестнадцатеричная

4
Скачать файл