3,14=3,14*100=0,314*101=0,0314*102=…
Порядок числа определяет положение запятой и записи мантиссы. При изменении порядка соответствующим образом меняется положение запятой. Запятая как бы «плавает». Это изменение запятой и дало название способу представления чисел.
Число с плавающей точкой представляется неоднозначно. Одно из этих представлений называется нормализованным. В этом случае для десятичной системы счисления мантисса должна удовлетворять требованию:
![]()
Другими словами, первая цифра мантиссы после запятой должна быть отличной нуля. Для числа 3,14 представление в нормализованной форме будет иметь следующий вид:
3,14=0,314*101
Здесь A=0,314, p=1. Аналогично для числа -0,00062 имеем -0,00062=0,62*10-3 A=0,62, p=-3.
Точно также в любой системе счисления с основанием Q число a неравное нулю записывается в форме с плавающей точкой. Число a называется нормализованным, если выполняется условие:
![]()
Пример 1.
Пример 1.
Дано A(10)=43,97. Найти A(2).
Решение:
Сначала переводим целую часть B(10)=43
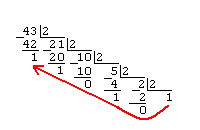
B(2)=101011
Затем дробную C(10)=97
C(2)= 1100001
Записываем результат
D(2)= 101011,1100001
Теперь приводим число к нормализованному виду. Для этого сдвигаем запятую на шесть разрядов 6(10)= 110(2).
Получили мантиссу равную 0,1010111100001 и порядок равный 110.
Ответ:
A(2)=0,1010111100001*10110
3.5. Арифметические операции в системах счисления используемых вычислительной техникой.
Все правила вычислений любой позиционной системы счисления совпадают с правилами десятичной системы счисления.
3.5.1. Арифметические операции с целыми числами в двоичной системе счисления.
Как и в десятичной системе счисления, все арифметические операции с целыми числами в двоичной системе счисления основаны на таблице сложения и умножения, приведенных в таблицах 6 и 7.
|
Таблица 6. Сложение двоичных чисел |
Таблица 7. Умножение двоичных чисел |
|||||
|
0 |
1 |
0 |
1 |
|||
|
0 |
0 |
1 |
0 |
0 |
0 |
|
|
1 |
1 |
10 |
1 |
0 |
1 |
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.