Основы алгоритмизации и вычислений: Учебно-практическое пособие, страница 27

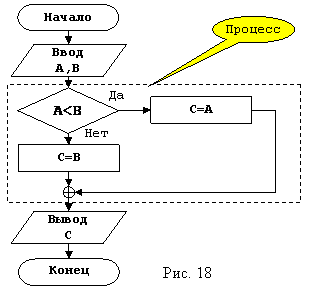
Как и в случае с линейным алгоритмом, сначала определимся с исходными данными. Из математического выражения видно, что исходные данных имеют символическое название A и B, и с результатами вычисления, исходя из того же выражения, это объект с именем C. Как и в предыдущем примере мы имеем два математически выражения, это C=A и C=B, однако исходное выражение содержит условие, то есть, в зависимости от исходных данным, в процессе выполнения алгоритма, должно быть выполнено только одно выражение. Если значение объекта A меньше значения объекта B, то выполнится первое выражение C=A, а если нет, то второе C=B. Получается, что в зависимости от исходных данных, алгоритм должен иметь два пути решения, либо выполняется первое выражение, либо второе.

Итак начинаем строить алгоритм решения поставленной задачи, рисунок 18. За основу как обычно берем общую структуру алгоритма, в блок «ввод данных» вводим символическое представление объектов, определенных как исходные данные, в нашем случае это A и B. Далее идет блок выполнения алгоритма. Поскольку поставленная задача может иметь два пути решения, вводим в блок процесса структуру развилки, и записываем в нее условие, которое является причиной различных путей решения, в нашем случае это A<B.Теперь у нас получилось два возможных пути решения, в случае выполнения условия, мы можем организовать один вычислительный процесс, а в случае его невыполнения другой, так и поступаем в случае выполнения условия организуем процесс, в котором будет выполняться шаг, выполняющий действие C=A, а в случае его невыполнения шаг на котором выполняется выражение C=B. После выполнения одного из возможных действий мы объединяем пути и организуем вывод результатов, для этого записываем в блок «результат» символическое название объекта, являющегося результирующим, в нашей задаче это объект C. На этом процесс построения алгоритма решения задачи можно считать завершенным.

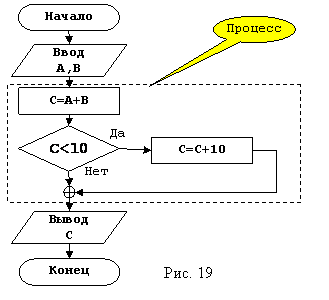Возможны варианты задач, в которых используется структура развилки, не имеющая  шагов, в случае невыполнения условий, например: C=A+B, если C<10, то C=C+10, графическое представление алгоритма приведено на рисунке 19. Как и в предыдущих примерах, определяемся с исходными данными, здесь они имеют символические названия A и B, и с результатами работы алгоритма, это объект, имеющий символическое название C. Теперь рассмотрим непосредственно процесс выполнения алгоритма. У нас имеется два выражения, это C=A+B и C=C+10, однако, первое выражение выполняется всегда, а второе, только при определенных исходных данных, в нашем случае условием C<10. Следовательно, нам необходимо внедрить развилку, но с одним условием, что дополнительный шал алгоритма, появляется только при выполнение условия развилки. В случае его невыполнения, дополнительные шаги не предусматриваются. Итак, анализ задачи проведен, теперь обращаемся к общей структуре алгоритма. В блок «ввод данных», как и в предыдущих примерах вносим список символических представлений объектов, являющихся исходными данным, в блок процесса, первым шагом, вычисление выражения C=A+B, далее идет блок развилки C<10, в случае выполнения которого, вводим дополнительный шаг C=C+10, и последним нашим действием, будет запись в блок «результаты» символического представления результатов работы алгоритма, в нашем случае это объект C. Процесс разработки алгоритма завершен.

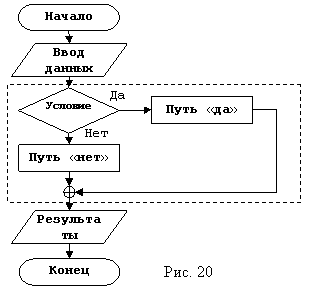
Общая структура алгоритма, использующего условное определение пути решения приведена на рисунке 20.

5.4.4. Структура цикла

Очень часто в жизни встречаются повторяющиеся процессы, тое есть процессы, состоящие из определенных шагов, повторяющиеся до тех пор, пока не выполнится какое либо условие. Так например, повторять набор номера телефона, до тех пор, пока не будет установлено соединение. Различаются три основных вида циклических процессов. Первое, это циклический процесс со счетчиком.. Этот вид циклического процесса подразумевает повторение одних и тех же операций, определенное число раз. Например, телефонный номер состоит из 10 цифр, то есть  для набора телефонного номера, нам необходимо ввести последовательность из 10 цифр. 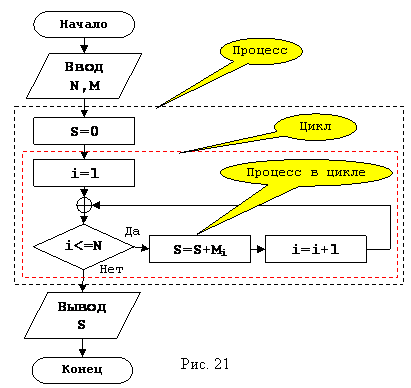Получается, что для набора номера телефона, мы используем цикл со счетчиком, то есть по очереди набираем цифры с первой по десятую. Рассмотрим простой арифметический пример, вычисление суммы чисел последовательности M размерности N, рисунок 21. Как и в предыдущих примерах сначала определяемся с исходными данными. В данной задаче первым делом определяемся с исходными данными. В данном случае, это размерность N и сама последовательность M. И с результатами работы алгоритма. В данном случае это сумма S. Далее непосредственно с процессом, выполняемым внутри алгоритма. Для определения суммы всех элементов какой либо последовательности нам необходимо их всех сложить. Для складывания всех элементов любой последовательности M необходимо перебрать их всех. Для перебора всех элементов любой последовательности необходимо организовать цикл со счетчиком. Счетчик в данном случае необходим для определения текущего номера элемента, а так же определения конца последовательности, и при каждом повторении цикла прибавлять значение элемента к символическому объекту, определяющему сумму. Кроме того, поскольку мы определяем сумму элементов, необходимо начальное значение символического объекта S приравнять нулю, поскольку при определении суммы цифра «0» не меняет результата. Общая структура цикла со счетчиком приведена на рисунке 22.