Как было сказано выше, существует три основных типа структур составляющих алгоритм это действие, условие и цикл. Рассмотрим теперь эти составляющие более детально.
5.4.2. Линейная структура алгоритмов
 Под понятием
«действие», можно понимать любую операцию. Если это операция в области
математики, то это может быть какая либо формула, если это операция в жизни
человека, то это какое либо его действие. Например положить монету в телефон-автомат
это действие или вычислит выражение c=a+b это тоже действие. Рассмотрим
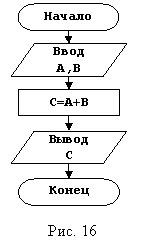
структуру алгоритма вычисления выражения C=A+B, приведенную на рисунке 16.
Под понятием
«действие», можно понимать любую операцию. Если это операция в области
математики, то это может быть какая либо формула, если это операция в жизни
человека, то это какое либо его действие. Например положить монету в телефон-автомат
это действие или вычислит выражение c=a+b это тоже действие. Рассмотрим
структуру алгоритма вычисления выражения C=A+B, приведенную на рисунке 16.
За основу берем общую структуру алгоритма, определяемся с исходными данными и результатами работы алгоритма. Для этого выражения исходные данные имеют символическое представление A и В, а результатом его работы будет сумма, имеющая символическое представление C. Следующим этапом необходимо определиться с процессом, который будет описывать алгоритм. В нашем случае, это вычисление суммы. Поставляем в общую структуру алгоритма наши выводы и получаем алгоритм вычисления суммы.
Рассмотренный пример содержит всего одно действие, по этому структура этого алгоритма получилась идентичной общей структуре алгоритмов.
Для более
детального понимания шага, классифицируемого как действие, рассмотрим структуру
алгоритма, состоящую не из одного, а из двух последовательных действий. Для
примера возьмем следующую последовательность вычислений: C=A+B, E=C*D, графическое представление
алгоритма которой 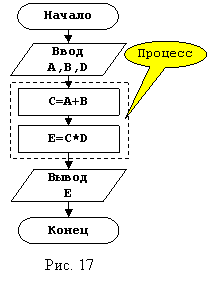 представлено на рисунке 17. Проанализируем наши исходные данные. В
первом выражении объекты(в данном случае числа) являющиеся исходными данными
имеют символическое представление A и B,
во втором выражении исходные данные имеют символическое представление C и D, однако
объект, имеющий символическое представление C является результатом первого выражения, а соответственно не
является исходными данными для алгоритма в целом. Следовательно исходными
данными алгоритма в целом являются объекты, имеющие символическое представление
A, B и D. Теперь разберемся с результатами работы алгоритма. В
первом выражении результатом работы является объект, имеющий символическое
представление C, а во втором объект, именуемый как E, однако объект C, является
промежуточным результатом работы алгоритма. Отсюда делаем вывод, что
результатом работы алгоритма является объект с символическим именем E. И последним этапом, идет анализ шагов, которые необходимо
проделать для получения конечного результата. В нашей задачи предусмотрено два
математических выражения, это C=A+B и E=C*D. Соответственно у нас должно быть два последовательных шага
типа «действие» первый это C=A+B, а второй E=C*D. Обращаемся к общей структуре алгоритма, описывающий любой
процесс. В блок «ввод данных» подставляем символические представления объектов,
используемых в качестве исходных данных задачи это A, B и D, в
качестве «процесса» вводим два последовательных действия это C=A+B и E=C*D. И наконец в блок «результаты»
подставляем символическое представление результирующих объектов, в нашем случае
это E. На этом процесс построения алгоритма решения
задачи можно считать завершенным. Структуры алгоритмов, имеющие только
последовательные действия имею общее название - линейные алгоритмы.
представлено на рисунке 17. Проанализируем наши исходные данные. В
первом выражении объекты(в данном случае числа) являющиеся исходными данными
имеют символическое представление A и B,
во втором выражении исходные данные имеют символическое представление C и D, однако
объект, имеющий символическое представление C является результатом первого выражения, а соответственно не
является исходными данными для алгоритма в целом. Следовательно исходными
данными алгоритма в целом являются объекты, имеющие символическое представление
A, B и D. Теперь разберемся с результатами работы алгоритма. В
первом выражении результатом работы является объект, имеющий символическое
представление C, а во втором объект, именуемый как E, однако объект C, является
промежуточным результатом работы алгоритма. Отсюда делаем вывод, что
результатом работы алгоритма является объект с символическим именем E. И последним этапом, идет анализ шагов, которые необходимо
проделать для получения конечного результата. В нашей задачи предусмотрено два
математических выражения, это C=A+B и E=C*D. Соответственно у нас должно быть два последовательных шага
типа «действие» первый это C=A+B, а второй E=C*D. Обращаемся к общей структуре алгоритма, описывающий любой
процесс. В блок «ввод данных» подставляем символические представления объектов,
используемых в качестве исходных данных задачи это A, B и D, в
качестве «процесса» вводим два последовательных действия это C=A+B и E=C*D. И наконец в блок «результаты»
подставляем символическое представление результирующих объектов, в нашем случае
это E. На этом процесс построения алгоритма решения
задачи можно считать завершенным. Структуры алгоритмов, имеющие только
последовательные действия имею общее название - линейные алгоритмы.
5.4.3. Структура развилки
В реальной жизни линейные или по другому безусловные алгоритмы встречаются крайне редко, поэтому в процесс алгоритмизации был введен второй вид шага, это шаг типа развилка. Шаг типа развилка предусматривает возможность внедрение в алгоритмы различные пути решения при различных исходных данных и ситуациях связанных с их обработкой. Другими словами шаг развилка это шаг проверки какого либо условия, если условие выполняется (то есть результат сравнения равен истине), то алгоритм идет по одному пути, если нет, то по другому. Рассмотрим этот вид алгоритмов на простом примере:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.